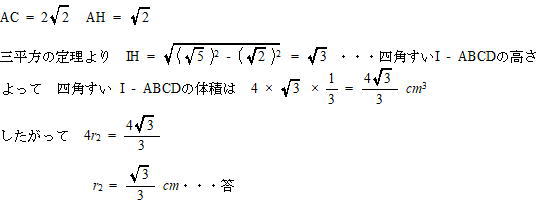青山学院高等部数学入試問題出題傾向と解説解答
高校受験はスペースONEのプロ家庭教師にお任せください。

青山学院高等部過去問傾向と対策

　　

青山学院高等部過去問研究

2022年度青山学院高等部募集人数　男女合わせて約80名に対し、応募者男子448名　女子600名　受験者男子371名　女子519名　合格者男子101名　女子102名でした。

一般入学入試問題は,大問8題構成で、1.四則計算　2.場合の数　3.関数　4.数の性質　5.平面図形　6.方程式の応用　7.場合の数　8.空間図形が出題されました。昨年度より1問増えましたが、難易度は例年通り。また出題内容も頻出問題である場合の数，関数，方程式の応用，平面図形が出題されました。過去問を繰り返し学習することが合格へ効果的です。

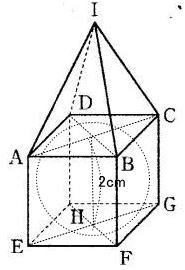
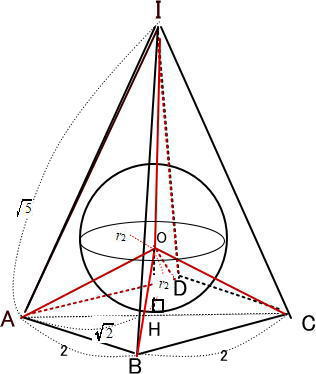
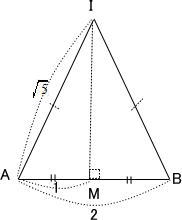
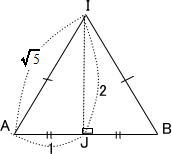
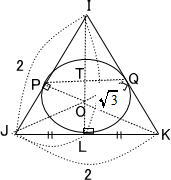
今回は　9.空間図形を解説します。　立方体に内接する球に関する問題は、高校受験でもよく出題されます。

　　　　　　　

青山学院高等部2022年度数学入試問題8.空間図形 問題

青山学院高等部2022年度数学入試問題8.空間図形 (1)解説解答

(1)　R1の半径r1を求めよ。

解説解答



立方体に内接する球の中心は　向かい合う正方形の対角線の中心を通るので

一辺2cmが球の直径になる。

よって　rr1 = 1cm


答　　1cm

青山学院高等部2022年度数学入試問題8.空間図形 (2)解説解答


(2)　R2の半径r2を求めよ。



内接円の中心をOとする。

四角すい I - ABCDの体積 = 四角すい O - ABCD の体積+ 三角すい O - ABIの体積 +三角すい O - BCIの体積 +三角すい O -CDIの体積 +三角すい O -DAIの体積

三角すい O - ABIの体積 = 三角すい O - BCIの体積 =三角すい O -CDIの体積 =三角すい O -DAIの体積 なので

四角すい I - ABCDの体積 = 四角すい O - ABCD の体積+ 三角すい O - ABIの体積 ×4

四角すい O -ABCDの底面積は　2×2 = 4c㎡　高さ = r2

三角すい O - ABIの底面積は　△ABI

三平方の定理より　△ABIの高さは



頂点Iから底面ABCDに垂線を下ろし、その交点をHとする。

Hは正方形ABCDの対角線の中点上にある。

△ABCは直角二等辺三角形なので








青山学院高等部2022年度数学入試問題8.空間図形 (3)解説解答



(3)　球R1が底面EFGHと接する点をN，⑨R2が側面IAB，ICDと接する点をそれぞれP，Qとするとき、△NPQの面積を求めよ。

解説解答

P，Qはそれぞれ△OABにおける∠AIB，△ICDにおける∠CIDの垂直二等分線上にある。



辺ABの中点をJとする。



同様にCDの中点をKとする。　IK = 2cm

直線JK = AD = BC = 2cm



JKの中点をJとする。

IJ = 2cm，JL = 1cm　なので



△POJ ≡ △LOJ ≡ △QOK ≡ △LOK　なので

jP = KL = KQ = KL = 1cm

PQの中点をTとする。

IP ＝PJ なので



△IPQ ∽ △IJK　　PQ：JK = 1：2 　JK = 2cmなので　PQ = 1cm







Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com