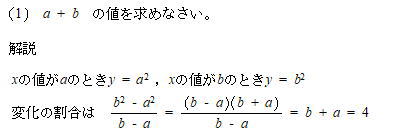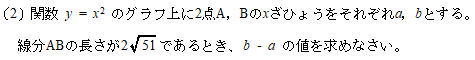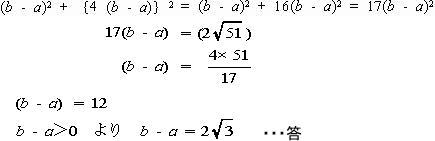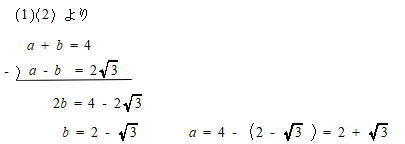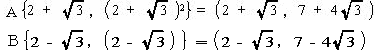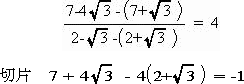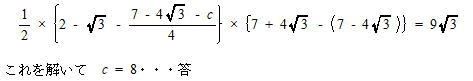慶應義塾高等学校過去問研究
2013年度慶應義塾高校数学入試問題は、小問集合・大問の出題構成で、昨年より大問が１問減りましたが枝問が増えましたが、全体のボリュームは例年通りでした。出題内容は １．小問集合５問 ２．関数のグラフと図形 ３．平面図形 ４．連立方程式の応用 ５．空間図形でした。
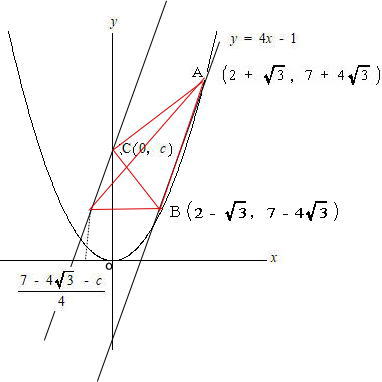
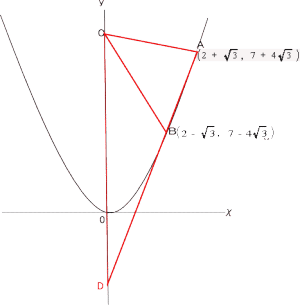
今回は 慶應義塾高校数学頻出問題 ２．関数のグラフと図形を解説します。
慶応義塾高校 過去問対策
出題内容は １．小問集合５問 ２．関数のグラフと図形 ３．平面図形 ４．連立方程式の応用 ５．空間図形でした。
今回は 慶應義塾高校数学頻出問題 ２．関数のグラフと図形を解説します。
