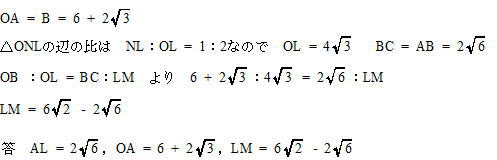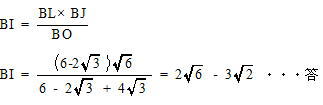慶應義塾女子高等学校数学過去問研究
慶応義塾女子高等学校は 一般入試・帰国生入試とも同一問題です。2013年度慶応義塾女子高等学校数学入試問題は1.小問2問 2.関数 3.整数の性質 4. 平面図形(円の性質) 5.立体図形が出題され、例年通りの大問5題構成で、出題内容も同一分野でした。また、例年通り証明問題がなく、整数問題が出題されました。解答形式は例年通り全問記述でした。
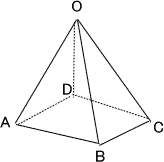
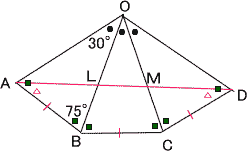
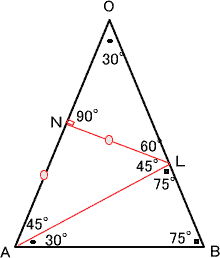
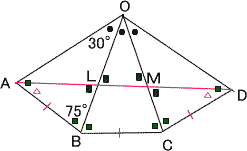
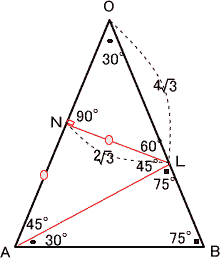
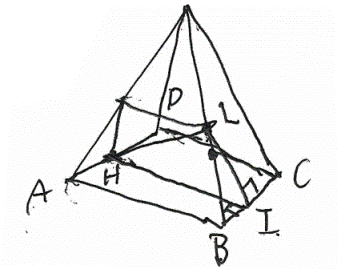
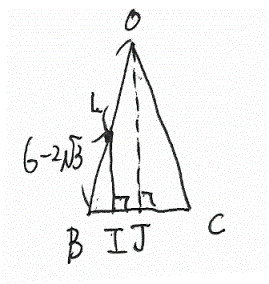
今回は4.立体図形を解説します。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
お問い合わせ
受付時間: 平日 AM 10:00 〜 PM 9:00