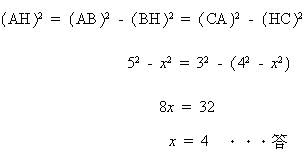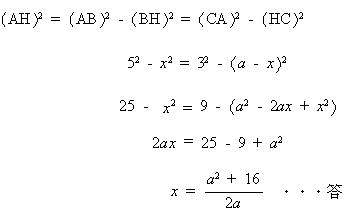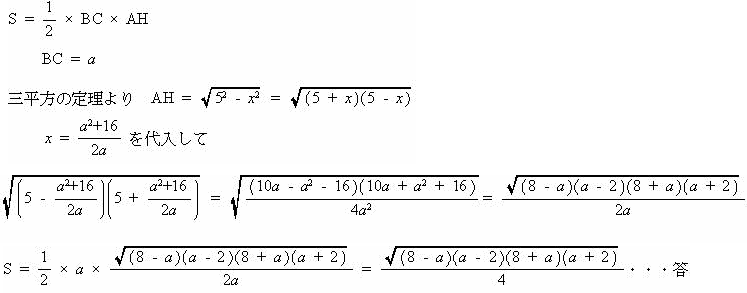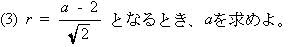慶應義塾志木高等学校過去問研究
2014年度慶應義塾志木高校数学入試問題は、小問集合がなくなり、大問のみの出題構成でしたが、枝問のない問題が3問あり、全体のボリュームは例年通りでした。
出題内容は １．数の性質 ２．関数 ３．方程式の応用 ４．平面図形証明 ５．平面図形 ６．平面図形（円の性質）７．確率でした。
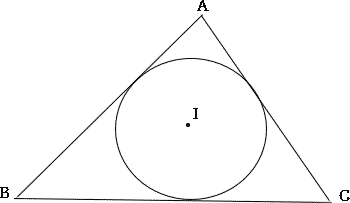
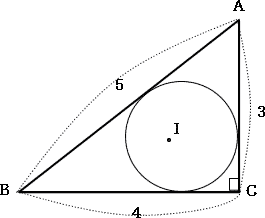
今回は 慶應義塾高校数学頻出問題 ６．平面図形（円の性質）を解説します。
出題内容は １．数の性質 ２．関数 ３．方程式の応用 ４．平面図形証明 ５．平面図形 ６．平面図形（円の性質）７．確率でした。
今回は 慶應義塾高校数学頻出問題 ６．平面図形（円の性質）を解説します。
慶応義塾志木高校合格のための入試概要と過去問傾向と対策へ
