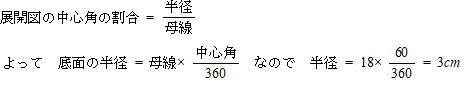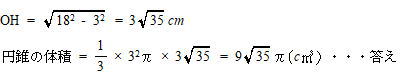東京都立国立高等学校独自作成問題傾向と対策
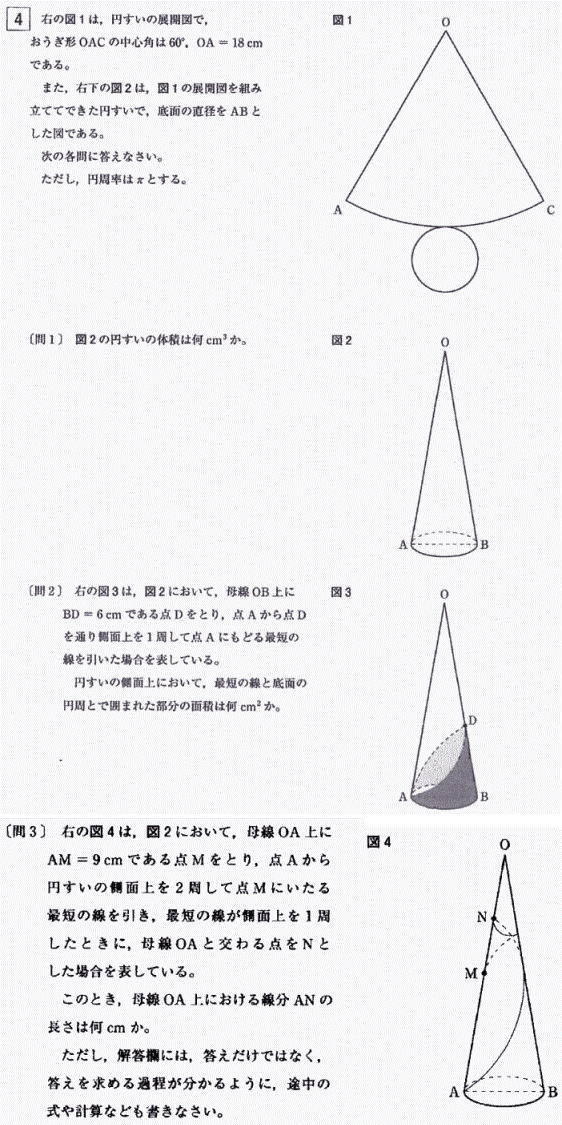
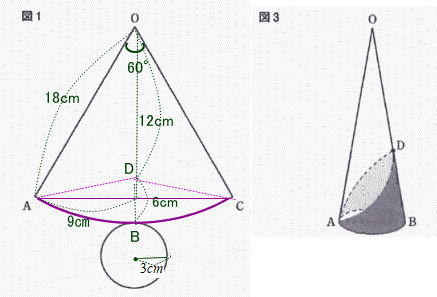
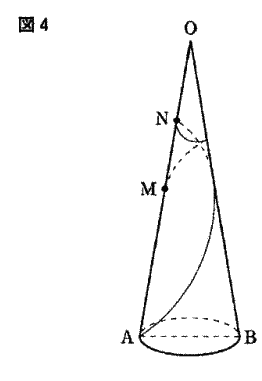
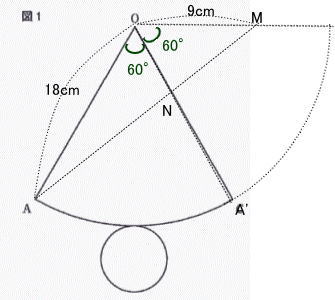
2009年度東京都立国立高等学校独自数学入試問題は 1.小問集合 2.平面図形 3.関数のグラフ 4.展開図と立体図形 4問構成でした。
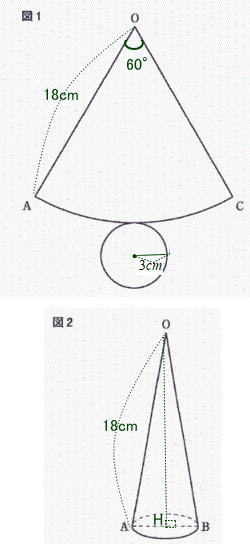
今回は4.展開図と立体図形を解説します。問1.2は解答のみ 問3は途中の式や計算を書く設問形式でした。問1.2は基本レベルです。教科書準拠問題集で一度は解いたことのある問題でしょう。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
お問い合わせ
受付時間: 平日 AM 10:00 〜 PM 9:00


2009年度東京都立国立高等学校独自数学入試問題は 1.小問集合 2.平面図形 3.関数のグラフ 4.展開図と立体図形 4問構成でした。
今回は4.展開図と立体図形を解説します。問1.2は解答のみ 問3は途中の式や計算を書く設問形式でした。問1.2は基本レベルです。教科書準拠問題集で一度は解いたことのある問題でしょう。