
明治大学付属中野高等学校過去問研究
2015年度明治大学付属中野高等学校数学入試問題は例年通りの出題構成で 1.計算問題合4問 2.小問集合6問 3.文章題2問 4.文章題 5.関数 6.平面図形が出題されました。文章題が2問出題され、立体図形の出題はありませんでした。
今回は 4.平面図形を解説します。補助線を利用して解きましょう。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
お問い合わせ
受付時間: 平日 AM 10:00 〜 PM 9:00


2015年度明治大学付属中野高等学校数学入試問題は例年通りの出題構成で 1.計算問題合4問 2.小問集合6問 3.文章題2問 4.文章題 5.関数 6.平面図形が出題されました。文章題が2問出題され、立体図形の出題はありませんでした。
今回は 4.平面図形を解説します。補助線を利用して解きましょう。
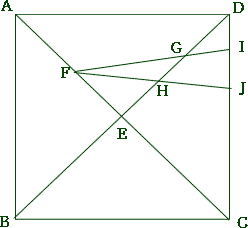
| (1) 線分DJの長さを求めなさい。 |
| 解説 |
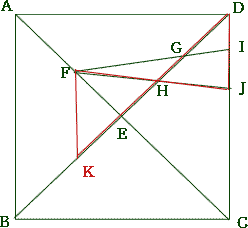 |
| 点FからDCに平行な直線をBD上にひき、その交点をKとする。 正方形の対角線は直交するので、∠FEK = 90° FK//DCより ∠FKE = ∠EDC = 45°(錯角) したがって △EDFは直角二等辺三角形  |
| (2) △FIJの面積を求めなさい。 |
| 解説 |
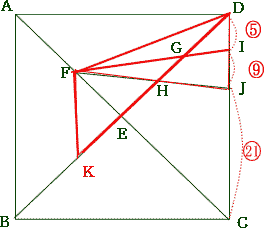 |
 |