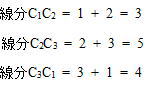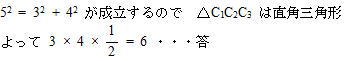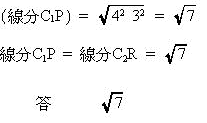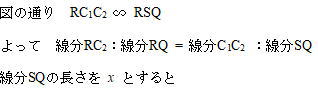明治学院高等学校一般入試数学過去問研究
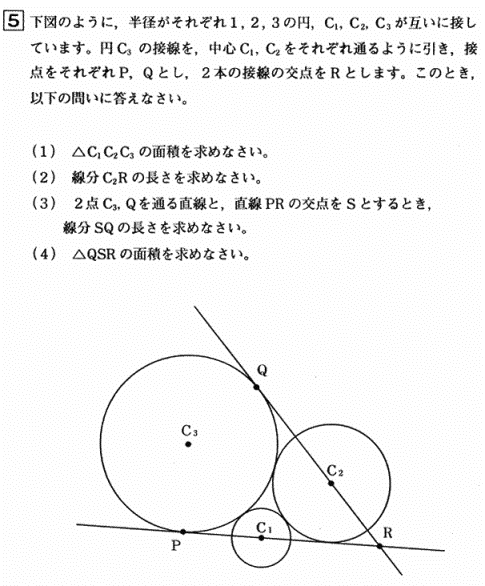
明治学院東村山高等学校の2012年度数学入試問題は 1.小問集合10問 2.場合の数 3.立体図形の切断 4.円周 5.円の性質 6.関数のグラフが出題され、昨年同様 大問6題構成で、答のみを記入する解答形式でした。
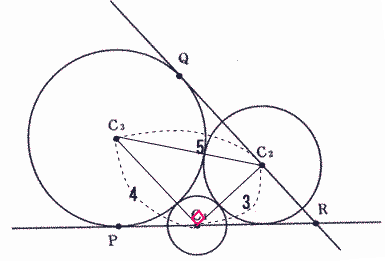
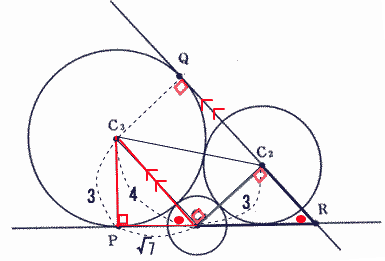
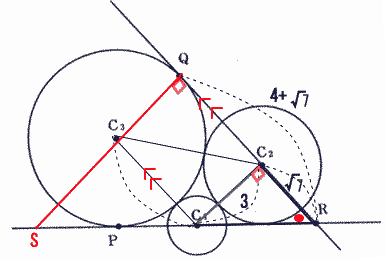
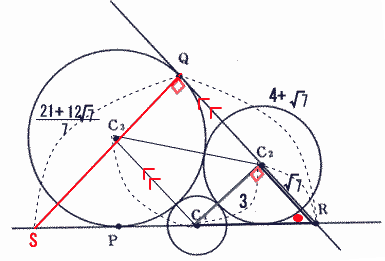
今回は5の円の性質を解説します。明治学院東村山高校数学入試問題は毎年大問で円の性質が出題され、受験生の正答率が低い問題です。特に2012年度は(2)の解答が出来ないと(3)(4)の解答が出来ず正答率が低くなってしまったようです。問5の問題の2012年度の受験生の正答率は(1) 77.1%, (2) 6.1%, (3) 1.7%, (4) 0.9%でした。
今回は5の円の性質を解説します。明治学院東村山高校数学入試問題は毎年大問で円の性質が出題され、受験生の正答率が低い問題です。特に2012年度は(2)の解答が出来ないと(3)(4)の解答が出来ず正答率が低くなってしまったようです。問5の問題の2012年度の受験生の正答率は(1) 77.1%, (2) 6.1%, (3) 1.7%, (4) 0.9%でした。