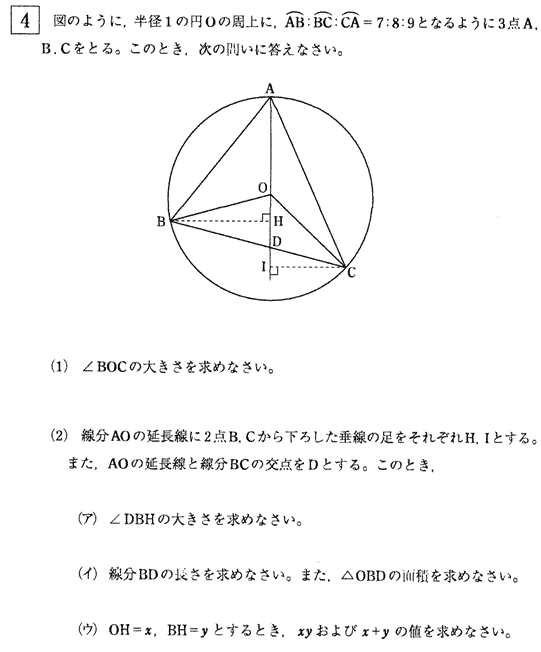
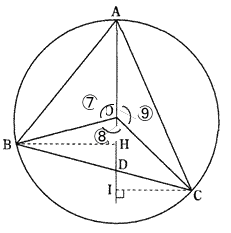
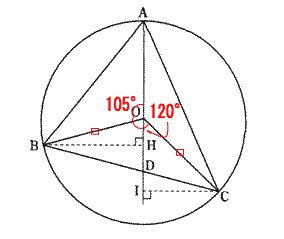
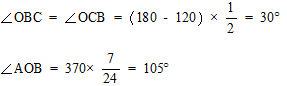有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

桜美林高校　過去問対策

2011年度桜美林高等学校数学入試問題(過去問) 解答解説

桜美林高等学校数学過去問研究
2011年度桜美林高等学校数学入試問題は例年通りの大問４問構成で、出題内容は１．小問集合9題　　２．一次関数と二次関数のグラフ　　３．速さの方程式とグラフ　　４．　円の性質でした。

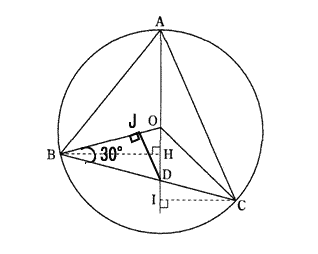
今回は４．円の性質を解説します。円の性質は桜美林高校数学入試の頻出問題です。基本的な円の性質を確認しましょう。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

桜美林高校2011年度　数学入試問題　4.　平面図形　問題

桜美林高校数学入試問題解説解答



桜美林高校2011年度　数学入試問題　4.　平面図形　(1)　解説解答

（1）　∠BOCの大きさを求めなさい。

解説

桜美林高校受験プロ家庭教師

中心角の大きさは弧の長さに比例するので

弧ＡＢ：弧ＢＣ：弧ＣＡ＝７：８：９　

高校受験プロ家庭教師

答　120°

桜美林高校2011年度　数学入試問題　4.　平面図形　(2)　解説解答

（2）　線分AOの延長線に2点B，Cから下ろした垂線の足をそれぞれH，I とする。

また，AOの延長線と線分BCの交点をDとする。

このとき，（ア） ∠DBHの大きさを求めなさい。

解説

桜美林高校受験プロ家庭教師
△BOCは　BO＝CO（半径）の二等辺三角形。

∠BOC＝120°なので　

高校入試プロ家庭教師東京

∠BOH＝180 - 105 = 75°

∠OBH = 90 - 75 = 15

よって　　∠DBH = 30 - 15 = 15°・・・答


（イ） 線分BDの長さを求めなさい。また，△OBDの面積を求めなさい。

線分BDの長さ　解説

△OBHと△DBHにおいて　　∠OBH＝∠DBH＝15°，∠OHB＝∠DHB＝90°，　BH＝BH（共通）なので　

△OBH≡△DBH

よって　OB＝１（半径）　　なので　OB＝DB＝１


△OBDの面積　解説

高校入試プロ家庭教師東京

図の通り　　点Dから辺BOに垂線をおろしその交点をJとする。　

△JBDは　∠JBD＝30°，∠BJD＝90°　よって　∠JDB＝60°

したがって　BD ： DJ の辺の比は ２：１　なので　　

高校受験プロ家庭教師

桜美林高校数学受験指導プロ家庭教師東京





Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com