
専修大学付属高等学校過去問研究
専修大学付属高等学校の2016年度数学入試問題は例年通り小問集合7題、大問4題構成でした。
出題内容は 1.独立小問7問 2.文章題(方程式の応用) 3.平面図形 4.関数のグラフ 5.平面上の点移動でした。
今回は 3.平面図形を解説します。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


出題内容は 1.独立小問7問 2.文章題(方程式の応用) 3.平面図形 4.関数のグラフ 5.平面上の点移動でした。
今回は 3.平面図形を解説します。
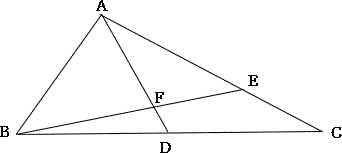
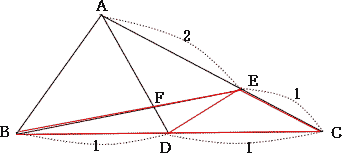
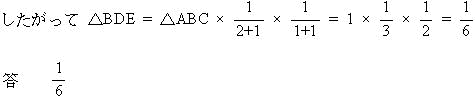
| (2) AF:FDをもっとも簡単な整数比で表しなさい。 |
| 解説 |
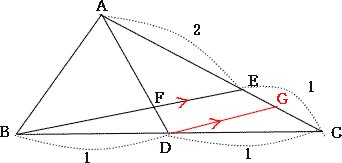 |
| DからACにBEと平行な直線を引き、その交点をGとする。 △CGD∽△CEBより CG:GE = CD:DB = 1:1 また △AFE∝△ADGより AF:FD = AE:FG AE:EC = 2:1なので したがって AE:EG = AF:FD = 4:1 |
| 答 4:1 |
| (3) △BDFの面積を求めなさい。 |
| 解説 |
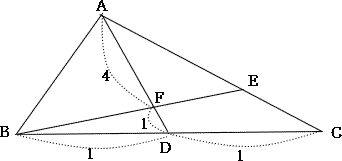 |
| BD:DC = 1:1 なので△ABD:△ADC = 1:1, AF:FD = 4:1 なので △ABF:△BDF = 4:1 したがって △BDFの面積は |