東邦大学付属東邦高等学校過去問研究
東邦大学付属東邦高等学校の2008年度数学入試問題は小問集合(6題)を含む大問6題構成でした。
全般的に平面図形の比重が増し立体図形が1題もありませんでした。
また、2008年度では証明問題も出されています。平面図形では相似条件・円の性質などを繰り返し練習しましょう

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


東邦大学付属東邦高等学校の2008年度数学入試問題は小問集合(6題)を含む大問6題構成でした。
全般的に平面図形の比重が増し立体図形が1題もありませんでした。
また、2008年度では証明問題も出されています。平面図形では相似条件・円の性質などを繰り返し練習しましょう
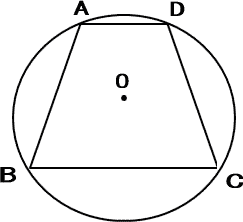
対応する2組の角がそれぞれ等しいことを利用して証明します。
∠ECBと∠OCFは共通ですから、角度を等しくするもう一組を見つけて証明します。
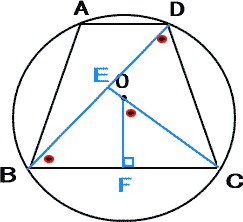
(証明)
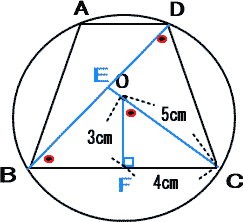
△BCDにおいて、 BC=CDより、∠EBC=∠EDC・・・①
![]()
また △OBCはOB=OC(円Oの半径)の二等辺三角形で、OFは頂点Oから底辺BCにひいた垂線であるので、∠BOF=∠COF
よって ∠BOC=2∠COF・・・③
② ③より ∠EOC=∠COF・・・④
① ④より ∠EBC=∠FOC・・・⑤
△BCEと△OCFにおいて ∠BCE=∠OCF(共通)
これと⑤より対応する2組の角がそれぞれ等しいので △BCE∽△OCF