高校受験指導専門プロ家庭教師の東京都立青山高等学校過去問研究
東京都立青山高等学校受験指導はスペースONEのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(本部・東京) |
03-6868-6040 |
|
お問い合わせ(福岡校) |
093-592-6658 |
 |
お問い合わせメール |
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
 HOME
HOME
2011年度東京都立青山高等学校入試問題(過去問) 解答解説
東京都立青山高等学校過去問研究
2011年度都立青山高等学校一般数学入試問題(自校作成問題)は例年通りの問題構成で、1.小問集合6問,2.関数のグラフ 3.平面図形 4.立体図形でした。
今回は 2.二次関数のグラフを解説します。
問題
スペースONEプロ家庭教師の解答で、東京都立青山高等学校の発表ではありません。
(1) 解説解答
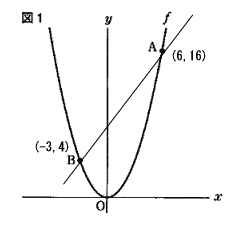
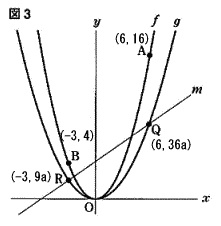
2点A,Bを通る直線の式を求めなさい。
|
|
| 解説 |
|
直線の傾きは (16-4)÷(6--3)=12/9=4/3
y=4/3χ+b に (6,16)を代入し b=16-4/3×6=8
|
 |
| 答 y=4/3χ+8 |
|
|
|
(2) 解説解答
 |
|
| 解説 |
|
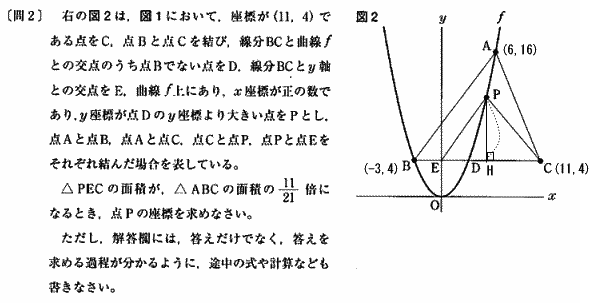
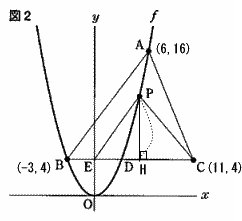
△ABCは 底辺(BC)=11+3=14, 高さ16-4=12
よって △PECの面積は 14×12÷2×11/21
点PからBCに垂線をおろし、その交点をHとすると
EC(11)×PH÷2=14×12÷2×11/21
PH=14×12×11/21÷11=8
よって 点Pのy座標は 8+4=12, χ座標は曲線f上の点なので 12=4/12・χ2
χ>0 より χ=6 |
 |
|
|
| 答 (6,12) |
|
|
|
(3) 解説解答
 |
|
| 解説 |
|
二次関数の変化の割合は
y=aχ2の式において、χの値が χ1からχ2まで増加するとき
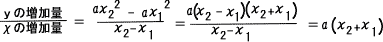 |
|
より、 y=4/9χ2で χの値がー3から0まで増加するときの変化の割合は 4/9{0+(-3)}=-4/3
点Rのχ座標が点Bと同じで、曲線g:y = aχ2上の点なので、点R(-3, 9a)
同様に 点Qのχ座標が点Aと同じで、曲線g:y = aχ2上の点なので、点Q(6, 36a)
よって 直線mの傾きは (36a - 9a)÷(6--3)= 27a/9 = 3a
-4/3×3a=-1 a=1/4 |
 |
| 答 1/4 |
|
|
|
HOME
Copyright(c)2007All Rights Rserved.
このホームページのすべての文章の文責および著作権はプロ家庭教師集団SPACE ONEに属します。

