
早稲田大学本庄高等学院過去問対策研究
平面図形問題で、三角形の頂点から底辺に垂線をおろし高さを求める問題は、高校受験の数学入試問題では典型問題です。平面図形が苦手な受験生は典型問題を繰り返し練習して受験対をとりましょう。
今回は2015年度早稲田大学本庄高等学院一般・帰国生数学入試問題[4]を解説します。
今回は2015年度早稲田大学本庄高等学院一般・帰国生数学入試問題[4]を解説します。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
お問い合わせメール
受付時間: 平日 AM 10:00 〜 PM 9:00


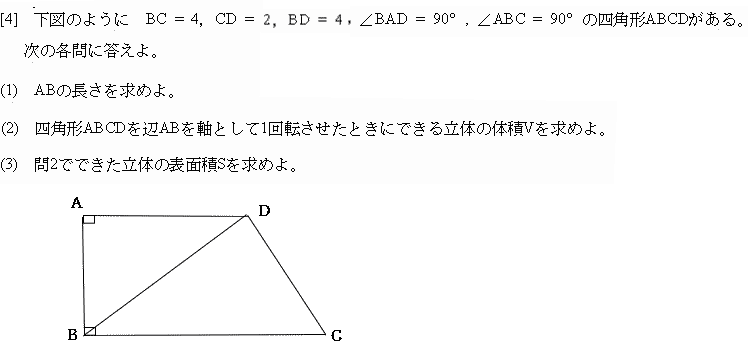
| (1) ABの長さを求めよ。 |
| 解説 |
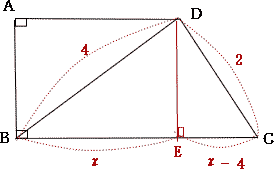 |
 |
| (2) 四角形ABCDを辺ABを軸として1回転させたときにできる立体の体積Vを求めよ |
| 解説 |
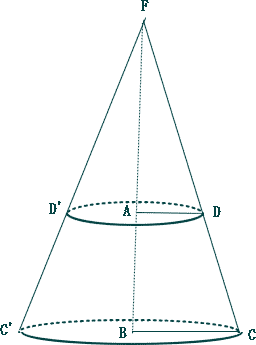 |
| 直線BAと直線CDの延長上の交点をFとする。辺ABを軸として1回転させたときにできる立体 = 円錐台は 図の通り、円錐F-CBC'から円錐F-DAD'を除いた部分。  |
| (3) 問2でできた立体の表面積Sを求めよ。 |
| 解説解答 |
 |
| AD:BC = 7:8なので、FD:FC = 7:8 DC = 2なので FC = 16  |