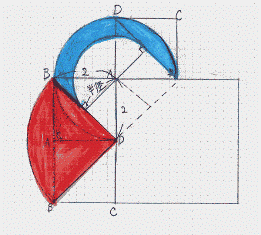久留米附設中学校・高等学校過去問対策

難関中学受験指導はスペースONEのプロ家庭教師にお任せください。

久留米附設中学校合格のための過去問傾向と対策

girl

久留米大学附属中学校過去問研究

久留米大学附属中学校2012年度入学試験は　志願者448名　合格者180名　合格者最高点 411点　合格者最低点284点　合格最低得点率 56.8%　合格者平均点 319点　受験者平均点 264点でした。

　算数入試問題は　１．四則計算を含む小問集合4問　２．規則性と場合の数　３．さいころの回転と面の数　４．文章題応用　駐車料金　５．回転図形　６．立体図形の切断が出題されました。
全て解答のみを記入する解答形式でした。

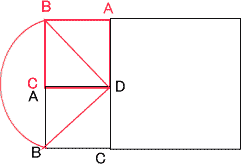
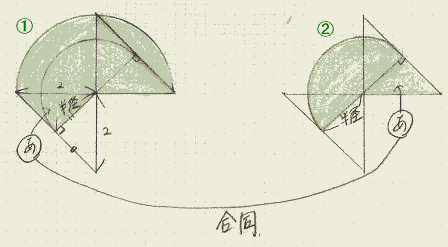
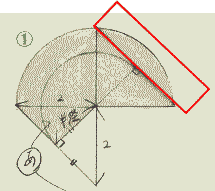
今回は　スペースＯＮＥ福岡校のプロ家庭教師が　５．回転図形を解説します。

算数入試問題　　回転図形

久留米大学付設中学校2012年度算数入試問題5.正方形の辺上の回転移動　問題


久留米大学付設中学校2012年度算数入試問題5.正方形の辺上の回転移動　(1)解説解答


(1)　最初の状態から頂点Ａが点Ｅにくるまでに、正方形ＡＢＣＤの対角線ＢＤが動いてできる図形の面積は何ｃ㎡ですか。

解説



図の通り　正方形ＡＢＣＤの対角線ＢＤを半径とする扇形の面積。



扇形の中心角は　∠CDA＝∠ADB＝45°なので　180ー45×2＝90°

正方形の面積より　BD×BD÷２＝一辺×一辺　なので

BD×BD＝２×２×２＝８

よって　　８×３．１４×90/360＝６．２８答　　　　６．２８ｃ㎡

久留米大学付設中学校2012年度算数入試問題5.正方形の辺上の回転移動　(2)解説解答

(2)　最初の状態から辺ＡＢが辺ＥＨにくっつくまでに、正方形ＡＢＣＤの対角線ＢＤが動いてできる図形の面積は何ｃ㎡ですか。

解説

最初の状態から辺ＡＢが辺ＥＨにくっつくまでに、正方形ＡＢＣＤの対角線ＢＤが動いてできる図形は　下図の通り。



②の半径は

直角二等辺三角形の面積より　

半径×半径÷２＝２×２÷２÷２なので　半径×半径＝２



問１からさらに加わった面積は　①から②の面積を除いた部分

①の面積は　半径２ｃｍの円の面積の1/2と三角形あを加えた部分。

②の面積は　半径×半径＝２の面積の1/2と三角形あを加えた部分部分。

あの面積は合同なので　結局増えた面積は

半径２ｃｍの円の面積から　半径×半径＝２の円の面積を除いた部分なので

２×２×３．１４÷２ー２×３．１４÷２
＝（２×２ー２）×３．１４÷２＝３．１４
よって　　６．２８＋３．１４＝９．４２


答　　　　９．４２ｃ㎡

久留米大学付設中学校2012年度算数入試問題5.正方形の辺上の回転移動　(3)解説解答


(3)　正方形ＡＢＣＤが正方形ＥＦＧＨの周りを１周して元にもどるとき、正方形ＡＢＣＤの対角線ＢＤが動いてできる図形の面積は何ｃ㎡ですか。

解説

図の通り　赤い部分と青い部分がそれぞれ４なので



赤い部分と青い部分の和は①の赤枠部分を除いた面積なので



赤枠部分の面積は２×２×３．１４×９０/３６０－２×２÷２＝１．１４（ｃ㎡）

よって　求める面積は　　　（９．４２ー１．１４）×４＝３３．１２


答　　　３３．１２ｃ㎡


Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com