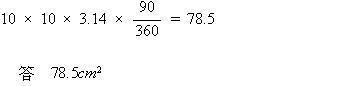九州国際大附属中学校過去問研究
九州国際大附属中学校2015年度算数入試問題は昨年同様 1.小問集合を含む大問5題構成でした。
中学受験に必要な基本的な知識を必要とする出題です。基礎力をつける毎日の努力が反映される出題内容です。
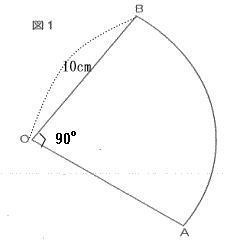
算数入試問題 5．平面図形の回転にチャレンジ
九州国際大学付属中学校合格のための過去問対策
九州国際大学付属中学校・高等学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
九州国際大学付属中学校2015年度算数入試問題5.平面図形 問題
九州国際大学付属中学校2015年度算数入試問題5.平面図形(1)解説解答
解説解答
おうぎ形の面積の求め方は
したがって
九州国際大学付属中学校2015年度算数入試問題5.平面図形(2) 解説解答
解説
三角形ＯＣＤと三角形ＯＡＤは
ＯＣ = ＯＡ = 10cm， ＣＤ = ＡＣ = 6cm， ＤＯ = ＤＯ = 8cm
三辺の長さがそれぞれ等しいので、合同な三角形。また、各辺の比より角ＣＤＯ = 角ＡＤＯ = 90°
また、ＢＥとＣＤは平行なので、 角ＢＥＯ = 角ＣＤＯ = 90°より 三角形ＯＢＥも直角三角形。
角ＥＯＢ + 角ＡＯＤ = 90°より
図のように一辺と両端の角度がそれぞれ等しいので三角形ＯＢＥと三角形ＯＡＤも合同な三角形。
したがって ＯＥ = ＣＤ = ＡＤ = 6cm
答 ６ｃｍ
九州国際大学付属中学校2015年度算数入試問題5.平面図形 (3) 解説解答
(3) 図2の三角形OBCの面積を求めなさい。
解説解答
三角形OBEと三角形CODは合同な三角形なので、図の通り×の部分が共通なので、三角形OBEと三角形CODの○の部分も同じ面積。
したがって 三角形OBCの面積（○ + □）と台形BEDC（○ + □）の面積も等しい。
台形BEDCの面積は上底６ｃｍ，下底８ｃｍ，高さ８ - ６ = ２ｃｍなので、
（６ + ８）×２÷２ = 14
三角形OBCの面積も 14c㎡
答 4c㎡
九州国際大学付属中学校2015年度算数入試問題5.平面図形 (4)解説解答
(4) 図2の斜線部分の面積を求めなさい。
解説
図2の斜線部分は中心角90°のおうぎ形OABの面積から三角形CBCと三角形OCDの面積と三角形OADの面積を除いた部分。
おうぎ形OABの面積は(1)から 78.5c㎡
三角形CBCの面積は(3)から 14c㎡
三角形OCDと三角形OADは合同な三角形で、底辺8cm,高さ6cmなので,面積は 8×6÷2×2 = 12c㎡
したがって 78.5 - (14 + 12) = 52.5
答 52.5c㎡