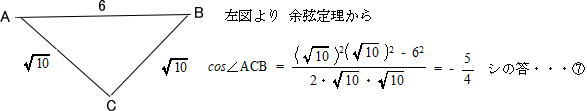こんにちは 大学受験専門プロ家庭教師の吉田です。
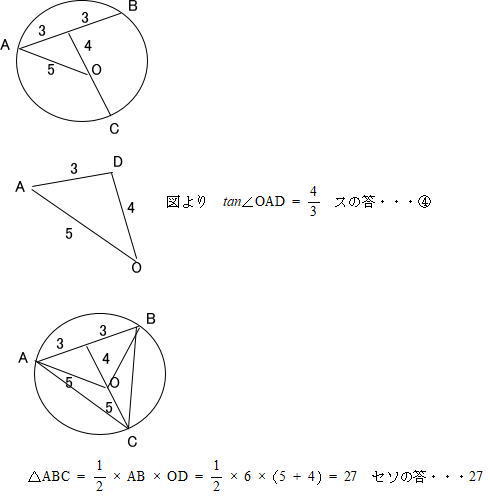
今回は 16日に実施された大学入学共通テスト2日目数学Ⅰ・数学Aから必答問題[1](2)定積分「円周上に頂点を持つ三角形の面積の最大値を求める問題」を解説します。
(1)で底辺の長さが一定のとき面積が最大になるのはどんなときかを考えましょう。
大学入学共通テスト過去問対策
大学入学共通テスト入試問題傾向と対策
大学受験はプロ家庭教師集団スペースONEにお任せください。
大学入学共通テスト2023年度数学Ⅰ・数学A[1](2)定積分 問題
大学入学共通テスト2023年度数学Ⅰ・数学A[1](2)(ⅰ)定積分解説解答
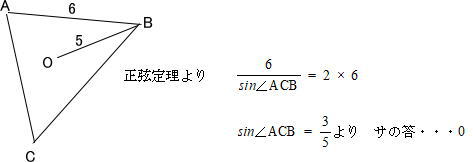
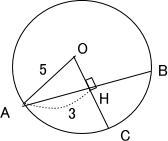CをOC⊥ABの位置にとっても cos∠ACBの大きさについての一般性は変わらない。
OCとABの交点をHとすると左図より OH = 4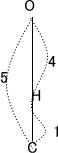
左図より HC = 1
大学入学共通テスト2023年度数学Ⅰ・数学A[1](2)(ⅱ)定積分解説解答
底辺AB = 6で一定だから 面積が最大となるのは高さが最大の時、それは下図のようにCがABの垂直二等分線と円との交点であるとき。
