北海道立高等学校数学過去問研究
今回は 北海道立高校2010年度数学入試問題４の二次関数のグラフを解説します。関数の座標と関数の式は高校入試の必出問題です。（１）（２）は基本問題、（３）は条件をグラフ上に書き込む面積分割問題です。
公立高校入試日まであと約２ヶ月。志望校の過去問で傾向をつかみ、類題を数多く解いて不得意問題に対応できるようにしましょう。
公立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
北海道立高校2010年度数学入試問題4.関数 問題
北海道立高校2010年度数学入試問題4.関数 (1) 解説解答
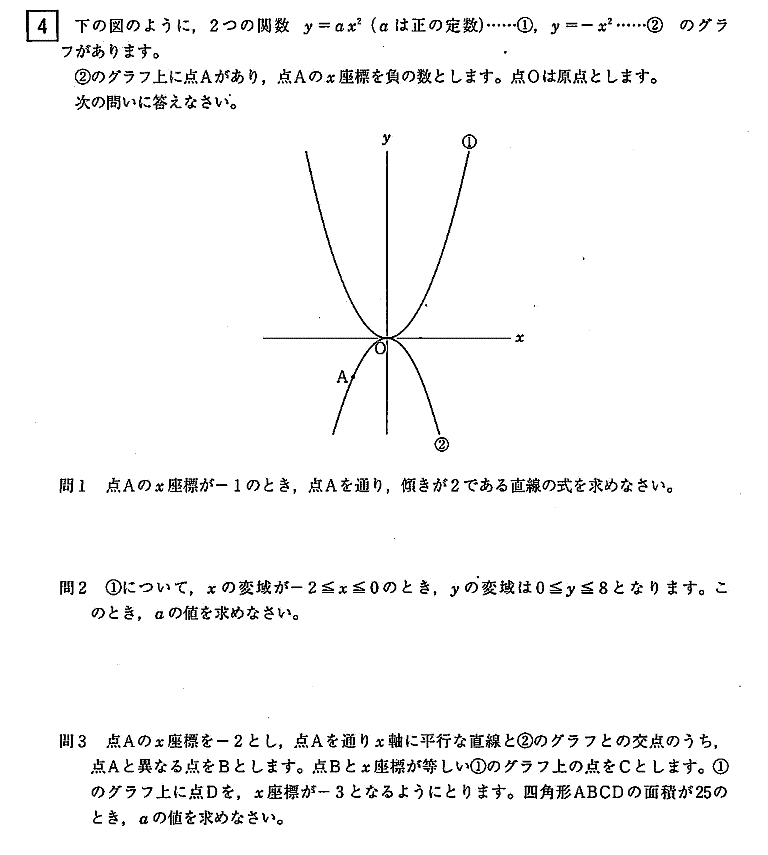
| 点Ａのχ座標がー１のとき、点Aを通り、傾きが２である直線の式を求めなさい。 |
| 解説 |
| 点Aはｙ＝－χ2上の点なので ｙ＝－１ |
| 傾きが２で（－１,－１）を通る直線の式は ｙ＝２χ＋ｂ にχ＝－１,ｙ＝－１を代入して ｂ＝１ |
| よって ｙ＝２χ＋１ |
| 答 ｙ＝２χ＋１ |
北海道立高校2010年度数学入試問題4.関数 (2) 解説解答
| ①について、χの変動がー２≦χ≦０のとき、ｙの変域は０≦ｙ≦８となります。このときａの値を求めなさい。 |
| 解説 |
 |
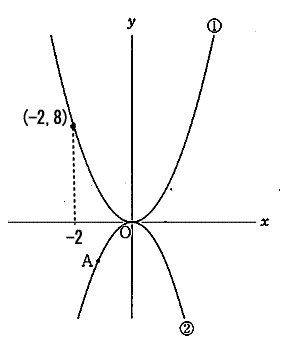| χの変動がー２≦χ≦０のとき、ｙの変域は０≦ｙ≦８なので、 ｙ＝ａχ2は（－２, ８）を通る放物線になる。 ｙ＝ａχ2に χ＝－２ ｙ＝８を代入して ８＝ａ×（－２）（－２）より ａ＝２ |
| 答 ２ |
北海道立高校2010年度数学入試問題4.関数 (3) 解説解答
| 点Aのχ座標をー２とし、点Aを通りχ軸に平行な直線と②のグラフとの交点のうち、点Aと異なる点をBとします。点Bとχ座標が等しい①のグラフ上の点をCとします。①のグラフ上に点Dを、χ座標がー３となるようにとります。四角形ABCDの面積が２５のとき、ａの値を求めなさい。 |
| 解説 |
| 条件に沿って考えていきましょう。 |
| 点Aのχ座標をー２とし、点Aを通りχ軸に平行な直線と②のグラフとの交点のうち、点Aと異なる点をBとします。 点Ａの座標は（-2, -4） 点Ｂは点Ａを通りχ軸に平行な直線と②のグラフとの交点なので 点Ｂのｙ座標も-4になる。 よって点Ｂの座標は（2, -4) |
| 点Bとχ座標が等しい①のグラフ上の点をCとします。 点Ｃのχ座標は２ また 点Ｃは①のグラフ上の点なので、 ｙ＝４a |
| ①のグラフ上に点Dを、χ座標がー３となるようにとります。 点Ｄのχ座標がー３なので、 ｙ座標は ｙ＝９a |
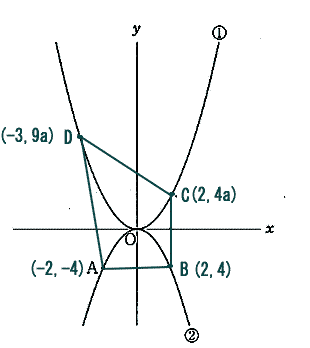
| 点Ａ，Ｂ，Ｃ，Ｄをグラフ上におくと下図の通り |
 |
 |
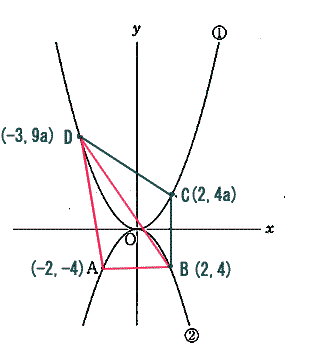| 四角形ABCDの面積が２５ 点ＢＤを直線で結ぶ。 三角形ＡＢＤと三角形ＢＣＤの面積の和が２５ 三角形ＡＢＤは底辺ＡＢ＝４、高さ９a＋４ 三角形ＢＣＤは底辺ＢＣ＝４a＋４、高さ３＋２＝５ よって ４×（９a＋４）÷２＋（４a＋４）×５÷２＝２５ これを解いて a＝1/4・・・答 |
