有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

市川高校合格のための過去問傾向と対策

市川高等学校過去問研究

2013年度市川高等学校数学入試問題は　大問6題構成。１．小問集合6問　2．円の性質　３．関数　４．文章題（方程式応用）　５．確率　６．平面図形　でした。出題形式・解答形式・難易度ともに例年通りでした。

数学の受験者平均点は　男子67.8点，女子64.7点, 全体66.7点でした。難問がないので、標準問題の全範囲を満遍なく学習すうことが、市川高校の数学の対策になるでしょう。

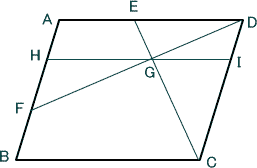
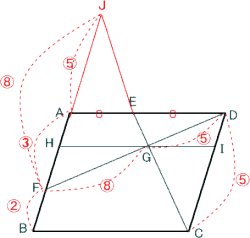
今回は　１小問集合から(6)の平面図形を解説します。


　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

市川高校2013年度数学入試問題　1(6)平面図形　問題

図のように、平行四辺形ＡＢＣＤがある。点Ｅは辺ＡＤの中点，点ＦはＡＦ：ＦＢ＝３：２となる点。

点Ｇは線分ＣＥとＤＦとの交点とする。

また、点Ｇを通り辺ＡＤに平行な直線と、辺ＡＢ，ＣＤの交点をそれぞれＨ，Ｉとする。

このとき、ＨＧ：ＧＩを最も簡単な整数の比で表しなさい。

市川高校受験プロ家庭教師千葉

市川高校2013年度数学入試問題　1(6)平面図形　解説解答

直線ＡＢの延長線と直線ＣＥの延長線との交点をＪとおく。


私立高校受験プロ家庭教師



△ＡＪＥ≡△ＤＣＥ（ＡＥ＝ＥＤ，∠ＪＡＥ＝∠ＣＤＥ，∠ＪＥＡ＝∠ＣＥＤ）

なので　ＪＡ＝ＤＣ＝ＡＦ＋ＦＢ　　よって　ＪＡ：ＤＣ：ＡＦ：ＦＢ＝５：５：３：３

△ＪＦＧ∽△ＣＤＧ（∠ＦＡＧ＝∠ＤＣＧ，∠ＪＧＦ＝∠ＣＧＤ）　

より　ＪＦ：ＣＤ＝ＦＧ：ＤＧ＝５＋３：５＝８：５

また△ＨＦＧ∽△ＩＤＧ（∠ＨＧＦ＝∠ＩＧＤ，∠ＧＨＦ＝∠ＧＩＤ）なので

ＨＧ：ＧＩ＝ＦＧ：ＧＤ

したがって　ＨＧ：ＧＩ＝８：５


答　　８：５




Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com