
神奈川県公立高等学校過去問研究
2015年度神奈川県立高校数学共通問題は例年通りの出題構成で. 1.四則計算2問 2.小問数号8問 3.関数 4.度数分布 5.立体図形 6.平面図形(円の性質)証明問題が出題されました。
今回は中学1年で学習する度数分布を解説します。
今回は中学1年で学習する度数分布を解説します。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


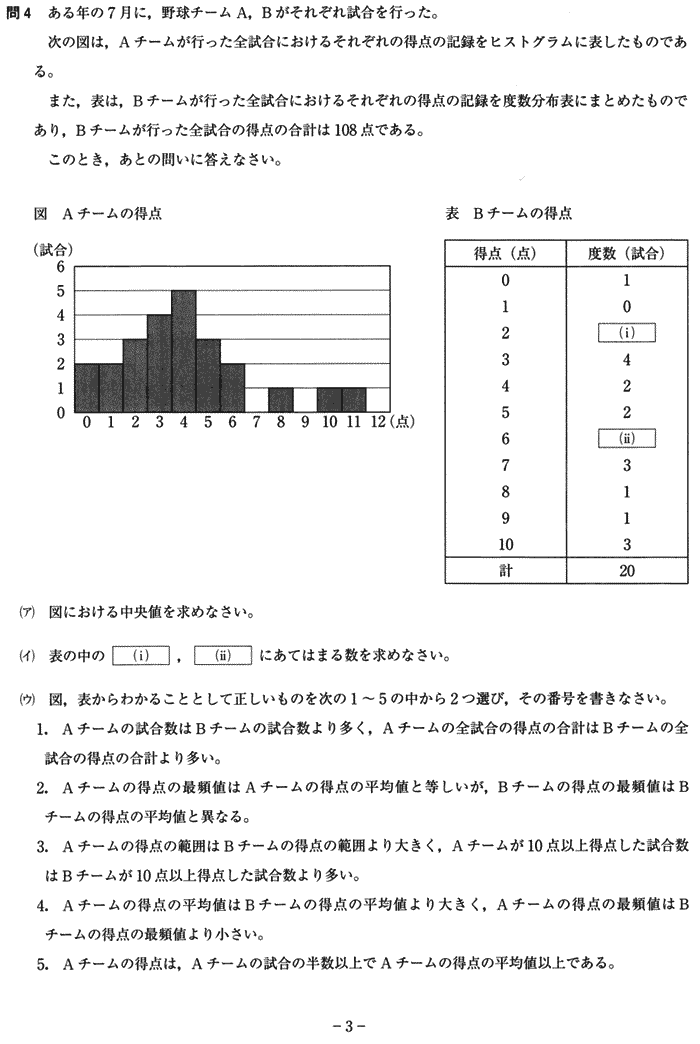
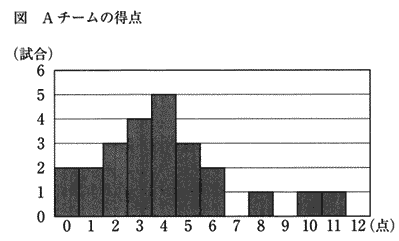
| (ア) 図における中央値を求めなさい。 |
| 解説 |
 |
| 中央値(メジアン):資料の値を大きさの順に並べたとき、中央にくる値。資料の個数が偶数のときは、中央の平均が中央値になる。 |
| Aチームの試合数は 2 + 2 + 3 + 4 + 5 + 3 + 2 + 1 + 1 + 1 = 24試合 |
| 中央にくる試合は (24 + 1 )÷2 = 12.5 |
| よって 中央値は12試合目13試合目のある4点 |
| 答 4点 |
| (イ) 表の中の[ⅰ][ⅱ]にあてはまる数を求めなさい。 |
| 解説 |
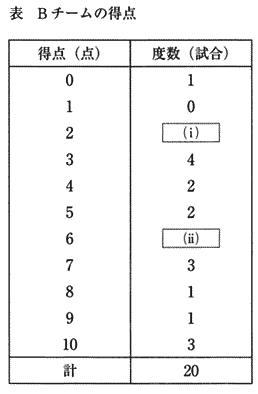 |
| 試合の合計は20試合なので 1 + 0 + [ⅰ] + 4 + 2 + 2 + [ⅱ] + 3 + 1 + 1 + 3 = 20 |
| [ⅰ] + [ⅱ] = 20 - ( 1 + 4 + 2 + 2 + 3 + 1 + 1 + 3) = 3 |
| また Bチームの得点の合計は108点なので 3×4 + 4×2 + 5×2 + 7×3 + 8 + 9 + 10×3 = 98点より |
| [ⅰ] + [ⅱ] の得点の合計は 108 - 98 = 10 |
| 3試合で 2点の試合数と6点の試合数になる組合せは 2点得点した試合数が2試合で6点得点した試合数が1試合のとき。 |
| 答 [ⅰ] 2, [ⅱ] 1 |
| (ウ) 図,表からわかることとして正しいものを次の1~5の中から2つ選び、その番号を書きなさい。 |
| 解説 |
| 1. Aチームの試合数はBチームの試合数より多く、Aチームの全試合の得点の合計はBチームの全試合の得点の合計より多い。 |
| Aチームの試合数は24,Bチームの試合数は20, Aチームの全試合の得点の合計は1×2 + 2×3 + 3×4 + 4×5 + 5×3 + 6×2 + 8 + 10 + 11 = 96点,Bチームの全試合の得点の合計は108点 したがって Bチームの全試合の得点の方がAチームより多い。 |
| 2. Aチームの得点の最頻値はAチームの得点の平均値と等しいが、Bチームの得点の最頻値はBチームの得点の平均値と異なる。 |
| Aチームの得点の最頻値も平均値も4点,Bチームの得点の最頻値4試合の3点だが、得点の平均値は5点。 |
| 3. Aチームの得点の範囲はBチームの得点の範囲より大きく、Aチームが10点以上得点した試合数はBチームが10点以上得点した試合数より多い。 |
| Aチームの得点の範囲は0点から12点,Bチームの得点の範囲は0点から10点でAチームの得点の範囲はBチームの得点の範囲より大きい。 Aチームが10点以上得点した試合数は2試合でBチームが10点以上得点した試合数は3試合でBチームの方がAチームより多い。 |
| 4. Aチームの得点の平均値はBチームの得点の平均値より大きく、Aチームの得点の最頻値はBチームの得点の最頻値より小さい。 |
| Aチームの得点の平均値は(1×2 + 2×3 + 3×4 + 4×5 + 5×3 + 6×2 + 8 + 10 + 11)÷24 = 4, Bチームの得点の平均値は108÷20 = 5.4, Aチームの得点の最頻値は4,Bチームの得点の最頻値は3, |
| 5. Aチームの得点は、Aチームの試合の半数以上でAチームの得点の平均値以上である。 |
| Aチームの得点の平均値は4,4点以上得点した試合数は4点(5試合)5点(3試合)6点(2試合)8点(1試合)10点(1試合)11点(1試合)計13試合。 |
| 答 2,5 |