
神奈川県公立高等学校過去問研究
2016年度神奈川県立高校数学共通問題は例年通りの出題構成で. 1.四則計算4問 2.小問集合8問 3.関数 4.確率 5.グラフ(列車の走行) 6.立体図形 7.平面図形(含 証明問題)が出題されました。
今回は4.確率を解説します。円周角の性質を確認しながら解きましょう。
今回は4.確率を解説します。円周角の性質を確認しながら解きましょう。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


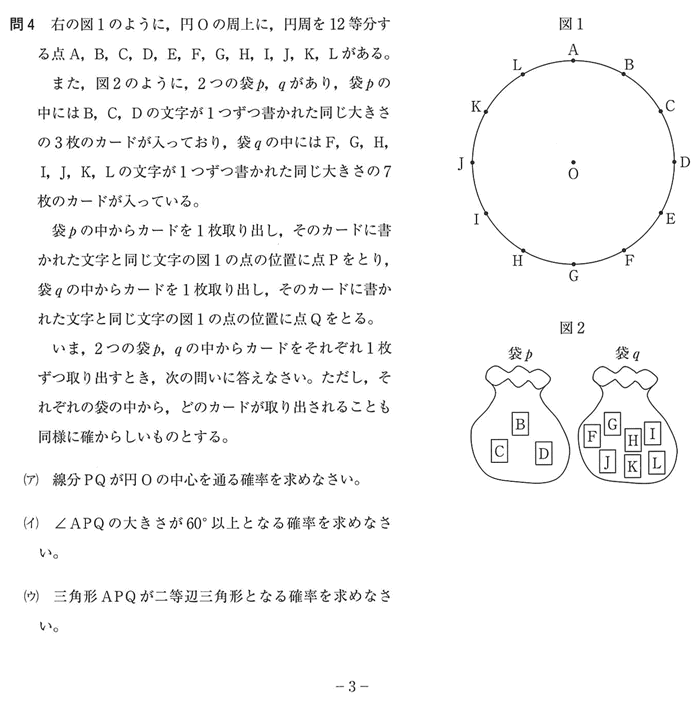
| (ア) 線分PQがOの中心を通る確率を求めなさい。 |
| 解説 |
| 起こりうる全ての場合の数 = カードの取り出し方は全部で(3×7)通り 線分PQがOの中心を通る場合は (p,q)とすると、(B,H),(C,I),(D,J)の3通り したがって 確率は |
| (イ) ∠APQの大きさが60°以上となる確立を求めなさい。 |
| 解説 |
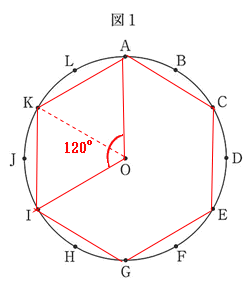 |
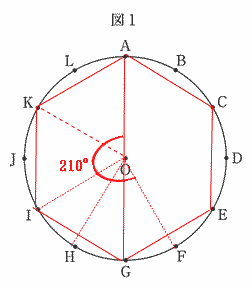
| 中心角と円周角の関係から、∠AOQが120°以上になるとき∠APQは60°以上になる。 点A,点B,点C,点D,点E,点F,点G,点H,点I,点J,点K,点Lを直線で結ぶと、正六角形になる。 よって ① ∠APQ = 60°になるのは、Q = Iのとき、弧AIの円周角 ∠ABI = ∠ACI = ∠ADI = 60°・・・3通り |
 |
|
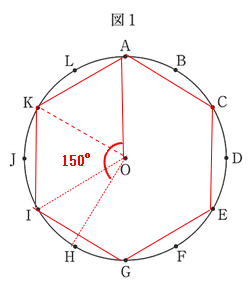
② ∠APQ = 75°になるのは、Q = Hのとき、弧AHの円周角 ∠ABH = ∠ACH = ∠ADH = 75°・・・3通り |
 |
|
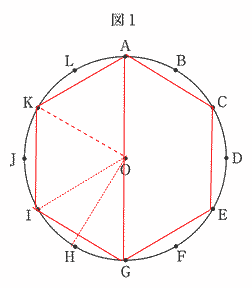
③ ∠APQ = 90°になるのは、Q = Gのとき、直径の円周角より ∠ABG = ∠ACG = ∠ADG = 90°・・・3通り |
 |
|
④ ∠APQ = 105°になるのは、Q = Fのとき、弧AFの円周角 ∠ABF = ∠ACF = ∠ADF = 105°・・・3通り |
|
①,②,③,④より 3×4 = 12通り したがって 確率は 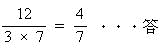 |
| (ウ) 三角形APQが二等辺三角形となる確立を求めなさい。 |
| 解説 |
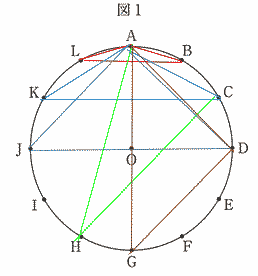 |
| P = Bのとき、AB = AL,1通り P = Cのとき、AC = AK,AH = CH,2通り P = Dのとき、AD = AJ,AD = GD,2通り よって 5通り したがって 確率は 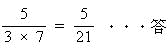 |