高校受験指導専門プロ家庭教師の東京都立国立高等学校過去問研究
東京都立国立高等学校受験指導はスペースONEのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(本部・東京) |
03-6868-6040 |
|
お問い合わせ(福岡校) |
093-592-6658 |
 |
お問い合わせメール |
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
 HOME
HOME
東京都立国立高等学校入試問題(過去問) 解答解説
東京都立国立高等学校過去問研究
2010年度東京都立国立高等学校独自数学入試問題は 1.小問集合6問 2.平面図形 3.関数のグラフ 4.立体図形。 例年通りの大問4題構成、出題構内容も例年通りでした。
昨年度は3.関数のグラフは二次関数が出題されましたが、今年度は一次関数となりました。
今回は3.一次関数のグラフを解説します。
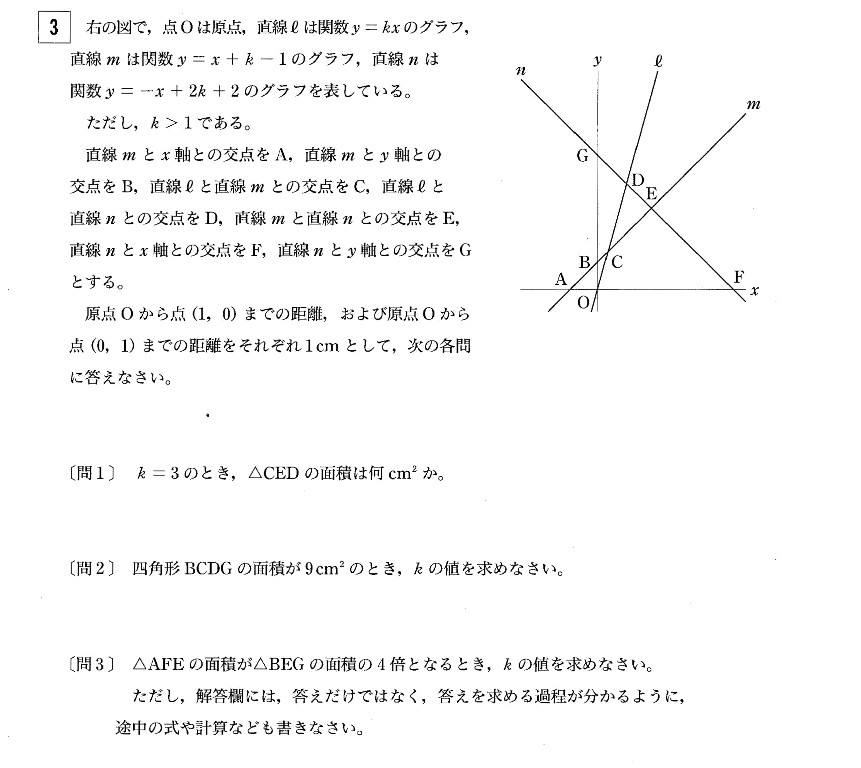
問題
スペースONEプロ家庭教師の解答で、東京都立国立高等学校の発表ではありません。
問1解説解答
| 問1 k= 3 のとき, △CEDの面積は何c㎡か。 |
|
| 解説 |
|
点Cの座標は 直線l:y=3χ と直線m:y=χ+2との交点なので、
C(1,3)
点Dの座標は 直線l:y=3χ と直線n:y=ーχ+8との交点なので
D(2, 6)
点Eの座標は 直線m:y=χ+2 と直線n:y=ーχ+8との交点なので
E(3, 5)
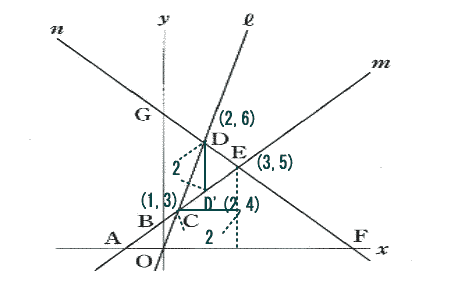
点Dからy軸に平行な直線を下ろし、直線mとの交点をD'とすると
D'の座標は χ=2より y=2+2=4
△CEDの面積は 1/2×DD'×(3-1)
1/2×(6-4)×(3-1)=2
|
 |
|
|
| 答 2c㎡ |
|
|
|
問2解説解答
| 問2 四角形BCDGの面積が9c㎡のとき、kの値を求めなさい。 |
|
|
|
| 解説 |
|
|
|
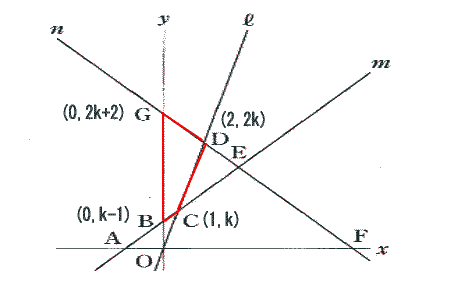
点Gの座標は直線nの切片なので(0, 2k+2)
点Bの座標は直線mの切片なので(0, k-1)
点Cの座標は直線lと直線mの交点なので、
kx=x+k-1
x(k-1)=k-1
x=1
y=k
点Dの座標は直線nと直線mの交点なので、
kx=ーx+2k+2
x(k+1)=2(k+1)
x=2
y=2k
□BCDG=△ODG-△OCB より
1/2×2×(2k+2)ー 1/2×1×(k-1)=9
k=13/3 |
 |
|
|
|
|
|
|
| 答 13/3 |
|
|
|
|
|
問3解説解答
| 問3 △AFEの面積が△BEGの面積の4倍になるとき、kの値を求めなさい。ただし、解答欄には、答だけではなく、答を求める過程が分かるように、途中の式や計算なども書きなさい。 |
|
|
| 解説 |
|
|
|
|
|
|
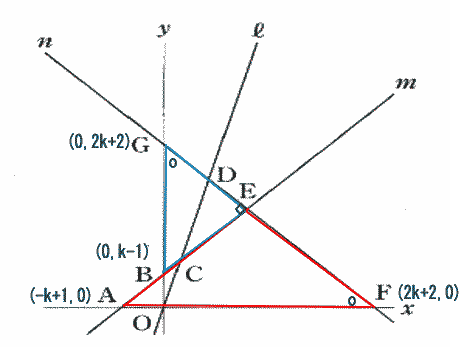
直線nの傾きは-1,直線mの傾きが1なので、AE⊥GF
よって ∠GEB=∠FEA=90°・・・①
また △GOFにおいて G(0,2k+2), F(2k+2,0) なので GO=FO, ∠GOF = 90°より △GOFは直角二等辺三角形
よって ∠EGB=∠EFA・・・②
①,②より ⊿AFE∽⊿BGE
⊿AFE:⊿GBE=4:1 なので
AF:BG=2:1
A(-k+1, 0) B(0,k-1)
AF=2k+2-(-k+1)=3k+1
BG=2k+2-(k-1)=k+3
したがって 3k+1:k+3=2:1
3k+1=2k+6
k=5 |
 |
|
|
|
|
|
|
| 答 k=5 |
|
|
|
|
|
HOME
Copyright(c)2007All Rights Rserved.
このホームページのすべての文章の文責および著作権はプロ家庭教師集団SPACE ONEに属します。