東京都立国立高等学校過去問研究
2011年度東京都立国立高等学校独自数学入試問題は 1．小問集合6問 2．二次関数のグラフ ３．平面図形 ４．一次関数のグラフ。 大問４題構成は例年通りでしたが、大問の立体図形が小問と４．一次関数のグラフになり、大問単体での出題はありませんでした。
今回は４．一次関数のグラフ（含、転回図形）を解説します。
都立国立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
都立国立高校2011年度 数学入試問題 4. 座標平面 問題
問１ 解説解答
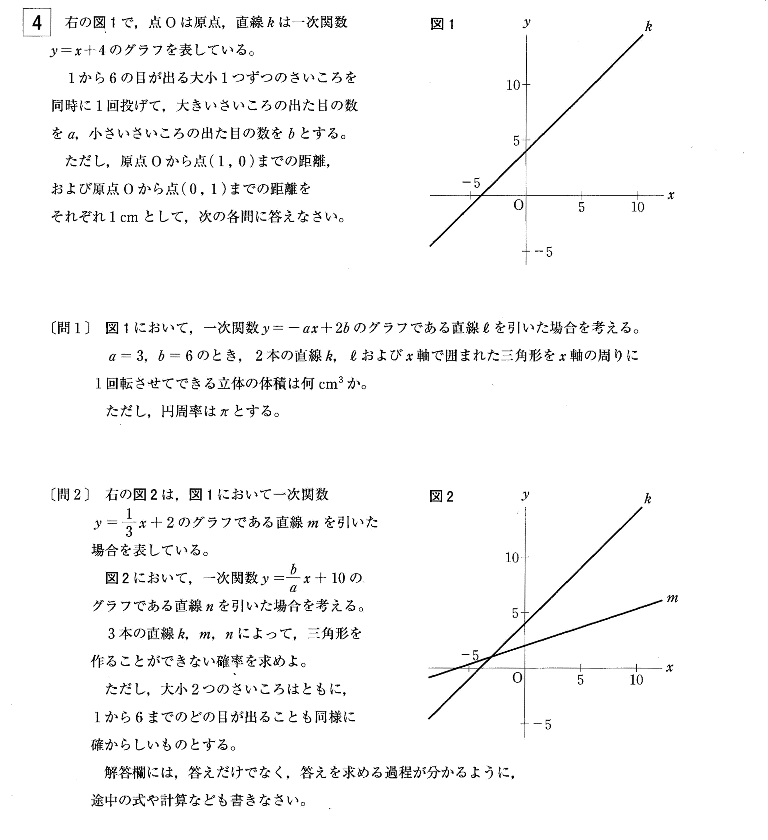
| 図１において、一次関数ｙ = -ax + 2b のグラフである直線ｌを引いた場合を考える。 a = 3， b = 6 のとき、２本の直線ｋ，ｌ およびχ軸で囲まれた三角形をχ軸の周りに１回転させてできる立体の体積は何ｃｍ3か。 ただし、円周率はπとする。  |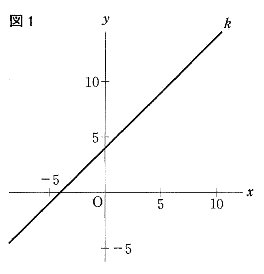
| 解説 |
 |
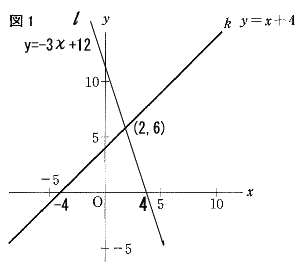| 直線ｌ：ｙ＝-3χ＋12と直線ｋ：ｙ＝χ+4 との交点の座標は（２，６） 直線ｌとχ軸との交点は -3χ＋12=0 より （４，０） 直線ｋとχ軸との交点は χ+4=0 より （－４，０） ２本の直線ｋ，ｌ およびχ軸で囲まれた三角形をχ軸の周りに１回転させてできる立体は錐なので、 ６・６π・８・1/3＝９６π |
| 答 ９６πｃm3 |
問２ 解説解答
 |
| 解説 |
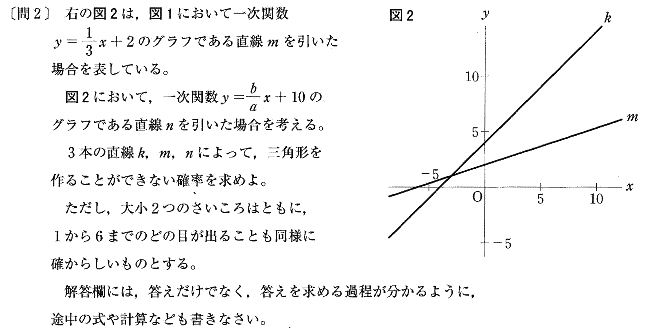
| 三角形を作ることのできない条件は ① ３直線が１点で交わるとき， ② ２直線が平行なとき なので ① ３直線が１点で交わるとき 直線ｋとｍとの交点の座標は 連立方程式 ｙ＝χ+4 と ｙ＝1/3χ+2 を解いて χ＝-3 ｙ＝１ よって （-3 , 1）（0 , 10）を通る直線の式は ｙ＝3χ+10 なので a,b の組み合わせは (a,b) = (1,3) (2,6) ② ２直線が平行なとき (ⅰ) 直線ｋと直線ｎが平行になるとき、 ｋの傾き１とｎの傾きも同じになるので a,b の組み合わせは (a,b) = (1,1) (2,2) (3,3) (4,4) (5,5) (6,6) (ⅱ) 直線ｍと直線ｎが平行になるとき、 ｍの傾き１/3とｎの傾きも同じになるので a,b の組み合わせは (a,b) = (3,1) (6,2) ① ②(ⅰ)(ⅱ)より 三角形を作ることのできない場合は(1,3) (2,6) (1,1) (2,2) (3,3) (4,4) (5,5) (6,6) (3,1) (6,2)の10通り。 よって 求める確率は 10/6・6＝5/18 |
| 答 5/18 |
