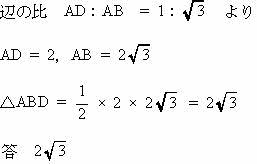有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、
不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

明治学院東村山高校　過去問対策

明治学院高等学校一般入試数学過去問研究

明治学院東村山高等学校の2014年度数学入試問題は、例年より大問が1題減り大問5題構成で　１．小問集合１0問　２．規則性　３．確率　４．平面図形　５．関数のグラフ　が出題され、例年通り、答のみを記入する解答形式でした。

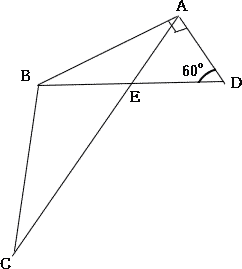
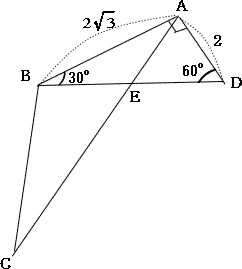
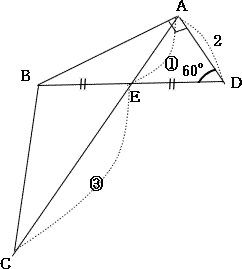
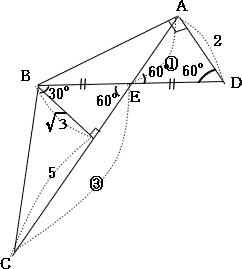
今回は４．平面図形を解説します。４．平面図形の2014年度の受験生の正答率は(1) 90.4％　(2)　34.5％　(3)12.2％でした。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

明治学院高校2014年度　数学入試問題　[4]　平面図形　問題


4.　AD ＝ 2 ，∠ B A D ＝ 90°，∠ ADB＝ 60°の直角三角形があります。

辺BD の中点を点E とし，直線AE の延長線上にAE：EC ＝１：３となるように点C を取りました。

点Cと点B を結んで右のような図を作ったとき，次の問いに答えなさい。

（１） △ ABD の面積を求めなさい。

（２） △ ABC の面積を求めなさい。

（３） 辺BC の長さを求めなさい。

明治学院東村山高校数学入試問題

明治学院高校2014年度　数学入試問題　[4]　平面図形　(1)　解説解答

（１） △ ABD の面積を求めなさい。

解説解答

中学数学平面

△ABDは∠ B A D ＝ 90°，∠ ADB＝ 60°，∠DBA = 30°の直角三角形なので、

高校入試プロ家庭教師東京数学専門


明治学院高校2014年度　数学入試問題　[4]　平面図形　(２)　解説解答


（２） △ ABC の面積を求めなさい。

解説解答

数学専門プロ家庭教師東京

BE：ED = 1：1　なので　△AEDと△AAEBの面積比も1：1

また　AE：EC = 1：3 なので　△ABE：△ABC = 1：1 + 3 = 1：4

したがって　△ABCの面積は

プロ家庭教師東京数学専門

明治学院高校2014年度　数学入試問題　[4]　平面図形　(3)　解説解答


（３） 辺BC の長さを求めなさい。

解説解答

平面図形中学数学

△ABDにおいて、辺の比より BD = 4， BE = EDなので　ED = 2

△ADEにおいて、AD = DE = 2，∠ADE = 60°なので、△ADEは正三角形。よって DE = 2,　∠BED = 60°(対頂角)

また頂点Bより辺CEに垂線を下ろしその交点をFとする。

△BEFは∠BEF = 60°,∠EFB = 90°より　∠FBE = 30°の直角三角形なので

数学専門プロ家庭教師東京神奈川千葉

Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com