武蔵野女子学院高等学校数学過去問研究
武蔵野女子学院高等学校は入学試験は 普通科総合進学コース，普通科薬学理系コース，普通科選抜文系コース，普通科国際交流コースがそれぞれ推薦試験・一般試験で選抜されます。
今回は、普通科薬学理系コースから、正答率3割強の図形問題大問3問を解説します。
都立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
武蔵野女子学院高校2015年度 数学入試問題 4. 5. 平面図形 問題
[4] 解説解答
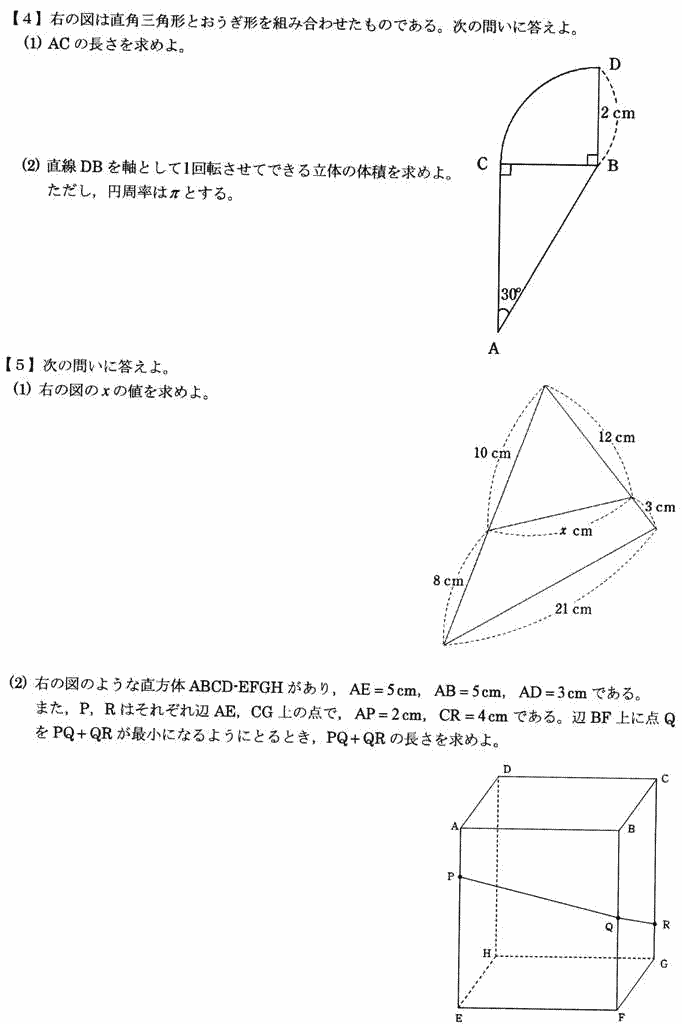
| （１） ＡＣの長さを求めよ。 |
| 解説 |
 |
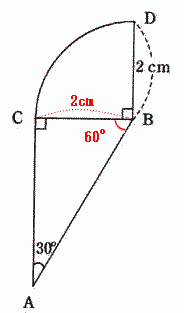| BC = BD = 2cm (おうぎ形の半径) △ACBは鋭角がそれぞれ30°，60°の直角三角形なので、 AC：CB の辺の比より  |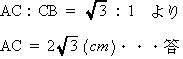
| (2) 直線CBを軸として1回転させてできる立体の体積を求めよ。ただし、円周率はπとする。（正答率36.9％) |
| 解説解答 |
 |
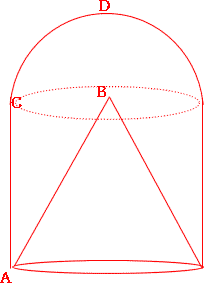１回転してできる立体は、右図の通り。 |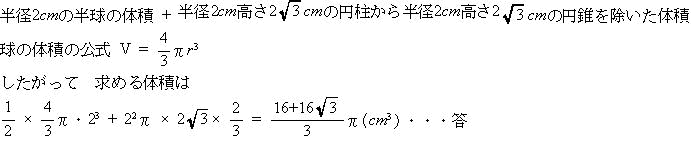
[5] (1) 解説解答
| (1) 右の図のχの値を求めよ。(正答率37.8％) |
| 解説解答 |
 |
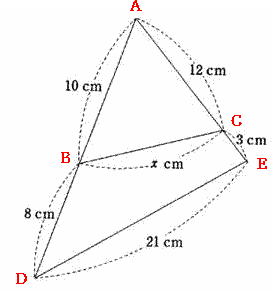| 図の通り A，B，C，D，Eとする。 △ABCと△AEDにおいて AB：AC = 10：12 = 5：6・・・① AE：AD = 12 + 3：10 + 8 = 5：6・・・② ∠CAB = ∠DAE (共通)・・・③ ①，②，③より２組の辺の比とその間の角がそれぞれ等しいので△ABC ∽ △AED したがって AB：BC = AE：ED 10：χ = 15：21 χ = 14 |
| 答 14 |
[5] (2) 解説解答
|
