灘高等学校過去問研究
2016年度灘高等学校数学入試問題は例年通り計算小問集合を含む大問6題構成でした。
小問集合は、途中式を書かない結果のみの解答形式です。解答時間は110分ありますが、大問5題はすべて難問揃いの記述形式です。基本問題は計算アドのケアレスミスをなくす注意深さが必要です。
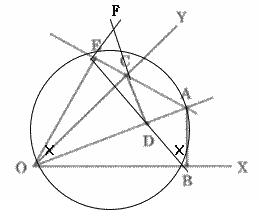
今回は、5.平面図形 証明問題3問を解説します。
灘高校過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
灘高校2016年度数学入試問題5.平面図形 問題
灘高校2016年度数学入試問題5.平面図形(1)解説解答
証明
灘高校2016年度数学入試問題5.平面図形(2) 解説解答
証明
灘高校2016年度数学入試問題5.平面図形 (3) 解説解答
(3) 2直線DC，OEの交点をＦとする。∠OBD = ∠OFCが成り立つことを証明せよ。
証明
(1) より ∠ABE = ∠AOE (弧ABの円周角)・・・⑤
(2)より3点B，D，Eは同一線上にあるので、∠OBD = 90°- ∠ABD = ∠ABE・・・⑥
∠OFC = 180°- ∠FDO - ∠DOF
(1)と仮定より ∠FDO = ∠CDO なので、
∠OFC = 180°- 90°- ∠DOF = 90°- ∠DOF = 90°- ∠AOE・・・⑦
⑤，⑥，⑦ より ∠OBD = ∠ODC
