高校受験指導専門プロ家庭教師の県立高等学校過去問研究
県立高等学校受験指導はスペースONEのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(本部・東京) |
03-6868-6040 |
|
お問い合わせ(福岡校) |
093-592-6658 |
 |
お問い合わせメール |
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
 HOME
HOME
2010年度県立高校入試問題(過去問) 解答解説
長崎県立高等学校数学過去問研究
今回は長崎県立高校の立体図穎の問題を解説します。三平方の定理を用いて解く問題です。体積を求める公式もあわせて復習しましょう。
問題 4
スペースONEプロ家庭教師の解答で、沖縄県の発表ではありません。
問1 解説解答
| 正四角すいOABCDの体積は何cm3か。 |
|
| 解説 |
|
| 錐の体積=底面積×高さ÷3より |
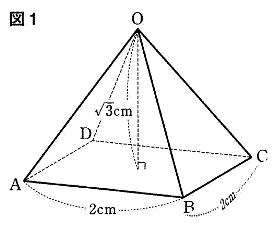 |
| 2×2×√3÷3=4√3/3 |
|
|
| 答 4√3/3cm3 |
|
|
|
問2 解説解答
| 辺OAの長さは何cmか。 |
|
| 解説 |
|
Oから底面ABCDに垂線をおろし底面との交点をHとすると、
図のように△AHBは直角三角形なので、
AH:AB=1:√2 より AH=√2
|
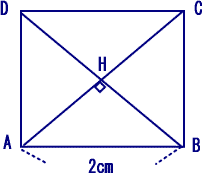 |
△OABも直角三角形なので 三平方の定理より
OA2=(√2)2+(√3)2
OA=√5 |
 |
| 答 √5cm |
|
|
|
|
|
(3)解説解答
| 三角形OABの面積は何c㎡か。 |
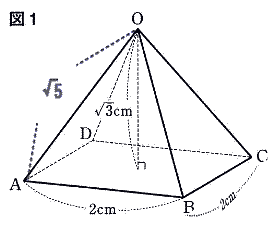 |
解答
|
|
Oから辺ABに垂線をおろしABとの交点をEとする。
⊿OAEは直角三角形なので、三平方の定理より
OE2=(√5)2ー12
OE=2cm
三角形OABの面積は
2×2÷2=2
|
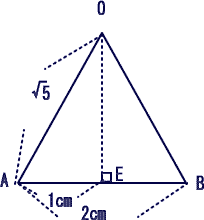 |
| 答 2c㎡ |
|
|
|
(4)解説解答
 |
| 解説 |
| 図の通り AP+PCが最小になるとき、辺OBと辺ACは直角に交わる。 |
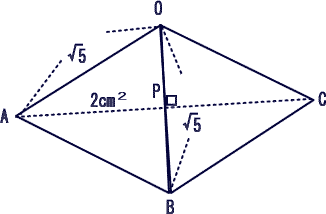 |
三角形OABの面積は 問3より2c㎡なので
AP=4√5/5
よって AP+PC=4√5/5×2=8√5/5
|
| 答 8√5/5cm |
|
|
HOME
Copyright(c)2007All Rights Rserved.
このホームページのすべての文章の文責および著作権はプロ家庭教師集団SPACE ONEに属します。

