
お茶の水女子大学付属高等学校過去問研究数学入試問題
お茶の水女子大附属高等学校の2017年度数学入試問題は大問5題構成で,1.小問集合6問 2. 関数とグラフ 3.平面図形(円の性質) 4.空間図形 5.平面図形(円周上の点移動)が出題されました。
今回は、5.平面図形(円周上の点移動)を解説します。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00



| (1) 出発して1秒後の点Pに注目する。図2のようにacm/秒とするとき、∠COAをaを用いて表しなさい。 |
| 解説解答 |
| 点Pが動く円周の長さは 6π,弧ACの長さはa 弧の長さとそれに対応する中心核の大きさは比例するので、 |
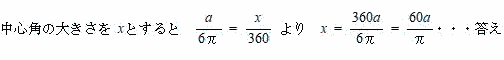 |
| (2) 出発してから初めて∠POQ = 30°となったのは、2秒後であった。点Pが円周を1周するのにかかる時間は何秒間か求めなさい。 |
| 解説解答 |
 |
| (3) 出発してから30秒後までの間に ∠POQ = 30°となる回数を求めなさい。 |
| 解説解答 |
| 点Pが円周を一周する時間は6秒。1秒ごとに360÷6 = 60°動く。 点Qが動く円周の長さは16πなので、点Qが円を一周する時間は 16π÷2π = 8秒 なので、1秒ごとに360÷8 = 45°動く。 1回目に∠POQ = 30°となるのは、(2)より2秒後 2回目に∠POQ = 30°となるのは、OPとOQの差が 360 - 30 = 330°開いたとき 330÷(60 - 45) = 22秒後 3回目に∠POQ = 30°となるのは、22秒後から点Pと点Qが同一線上にあり、さらに30°ひらいたときなので、 22 + 60÷15 = 26秒後 4回目に∠POQ = 30°となるのは、3回目からさらに差が300°開いたときなので、 出発してから30秒後までの間に ∠POQ = 30°となるのは、2秒後,22秒後, 26秒後の3回 |
| 答 3回 |