福岡大学附属大濠高等学校過去問研究
2012年度福岡大学附属大濠高等学校の数学入試問題は 例年通りの大問５題構成で、1. 2. 小問集合 ３．関数のグラフ ４．円の性質 ５．立体図形 の出題でした。
今回は スペースONE福岡校のプロ家庭教師が ４．円の性質を解説します。
今回は スペースONE福岡校のプロ家庭教師が ４．円の性質を解説します。
福岡大学付属大濠高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
福岡大学付属大濠高校2012年度 数学入試問題 4. 平面図形 問題
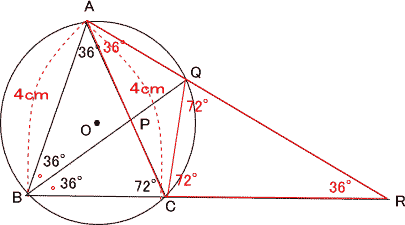
| 右の図のように∠BAC＝３６°，AB＝AC＝４ｃｍである二等辺三角形ABCの外接円Oがある。 ∠ABCの二等分線と辺AC，円Oとの交点をそれぞれ点P，Qとし，２直線AQ，BCの交点をRとする。 次の各問いに答えよ。 |
 |
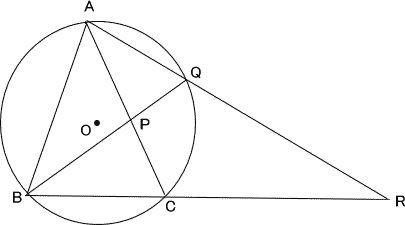| （１） ∠APQ＝[⑯]である。 | |
| （２） ∠RQC＝[⑰]である。 | |
| （３） 線分CRの長さは[⑱]ｃｍである。 | |
| （４） 辺BCの長さは[⑲]ｃｍである。 | |
| （５） RQ：RA＝[⑳]である。 |
福岡大学付属大濠高校2012年度数学入試問題 (1) 解説解答
| （１） ∠APQ＝[⑯]である。 | |
| 解説 | |
| △ABCは二等辺三角形なので ∠ABC＝∠ACB＝（180ー36)÷２＝７２ ＢＱは∠ABCの二等分線なので ∠ＡＢＰ＝∠ＣＢＰ＝７２÷２＝３６ △ABPにおいて ∠APQは∠APBの外角なので ∠APQ＝∠PAB＋∠ABP＝３６＋３６＝７２ |
 |
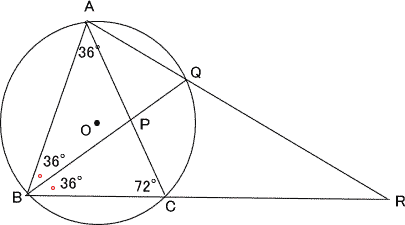| 答 ７２° |
(2) 解説解答
| （２） ∠RQC＝[⑰]である。 | |
| 解説 | |
| 円に内接する四角形では、 | |
| ① 対角の和は180°である。 |  |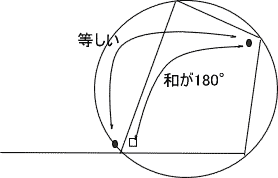
| ② 対角は、それととなり合う内角の対角に等しい。 | |
| よって | |
| ∠RQC＝∠ＡＢＣ＝72° |  |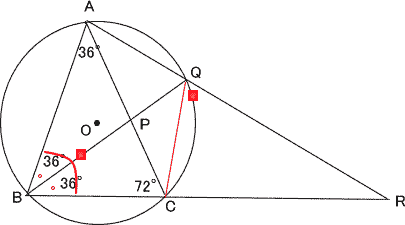
| 答 ７２° | |
(3) 解説解答
| （３） 線分CRの長さは[⑱]ｃｍである。 | |
| 解説 | |
| (2)より ∠RQC＝72° ∠RＣＱ＝∠ＢＡＣ＋∠CＡＱ ∠ＣＡＱ＝∠ＣＢＱ＝３６° なので ∠ＲＣＱ＝３６＋３６＝７２° よって ∠ＣＲＱ＝１８０－７２×２＝３６° △ＡＣＲにおいて ∠ＣＡＲ＝∠ＣＲＡ＝３６° なので △ＡＣＲは二等辺三角形 よって ＡＣ＝ＲＣ＝４ｃｍ |
 |
| 答 ４ｃｍ |
| (４） 辺BCの長さは[⑲]ｃｍである。 | |
| 解説 | |
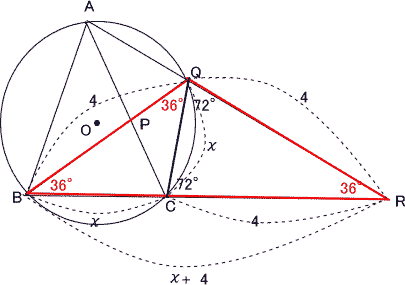
| 図の通り △ＣＱＢ∽△QBR BC＝χとおくと CQ：QB＝QB：BR なので χ：４＝４：（χ＋４） χ2＋４χ－16＝０ 解の公式より χ＝-2±2√5 BC＞０ より χ＝-2＋2√5 |
 |
| 答 -2＋2√5 |
| （５） RQ：RA＝[⑳]である。 | |
| 解説 | |
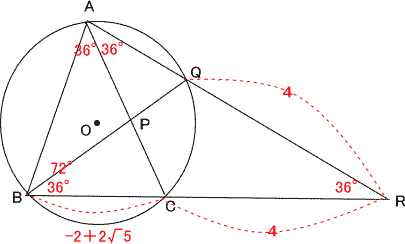
| ∠BAC＝３６° ∠ＣＢＱ＝∠ＣＡＱ＝３６°（弧ＱＣの円周角） ∠ＢＡＲ＝∠ＢＡＣ＋∠ＣＡＱ＝７２° よって △ＡＢＲは∠ＲＡＢ＝∠ＲＢＡなので二等辺三角形より ＲＢ＝ＲＡ＝４＋（ー２＋２√5） ＲＱ：ＲＡ＝４：２＋２√５ ＝２：１＋√5 |
 |
| 答 ２：１＋√5 |
