福岡大学附属大濠高等学校受験指導はスペースＯＮＥ福岡校のプロ家庭教師にお任せください。

	ご依頼専用ダイヤル	0120-604-405
	お問い合わせ(本部・東京)	03-6868-6040
	お問い合わせ(福岡校)	093-592-6658
	お問い合わせメール
	ws-spaceone

プロ家庭教師集団スペースONE

HOME

2015年度福岡大学附属大濠高等学校数学入試問題解答解説

福岡大学附属大濠高等学校過去問研究

2015年度福岡大学附属大濠高等学校の数学入試問題は　例年通りの大問５題構成で、1. 2. 小問集合　　３．関数のグラフ　４．平面図形　５．立体図形　の出題でした。

基本問題や高校数学入試では典型的な問題が出題されています。他校を受験する生徒にとっても復習となる問題揃いです。

今回は　スペースONE福岡校のプロ家庭教師が　４．平面図形を解説します。　

問題4

、

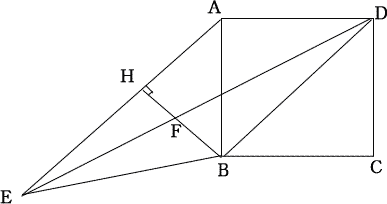
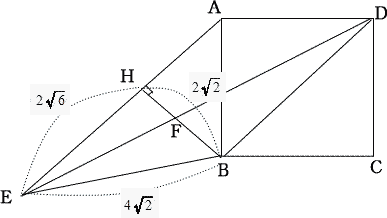
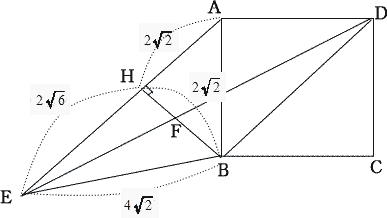
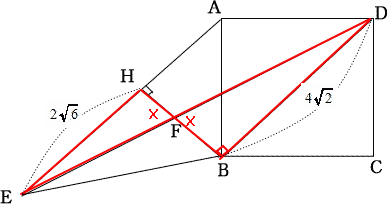
右の図のように、一辺の長さが4cmの正方形ABCDと三角形AEBにおいて、AE//DB，BD = BE，点Bから辺AEに垂線BHを引き、垂線BHと線分DEの交点をFとする。
次の各問いに答えよ。

(1)∠EABの大きさは[⑯]度である。

(2)線分BHの長さは[⑰]である。

(3)∠AEBの大きさは[⑱]度である。

(4)三角形AEBの面積は[⑲]c㎡である。

(5)三角形FEHと三角形FBDの面積の比を最も簡単な整数で表すと、(三角形FEH)：(三角形FDB) = [⑳]である。

スペースＯＮＥプロ家庭教師の解答で、福岡大学附属大濠高等学校の発表ではありません。

　

(1)　解答

(1)　∠EABの大きさは[⑯]度である。
解答
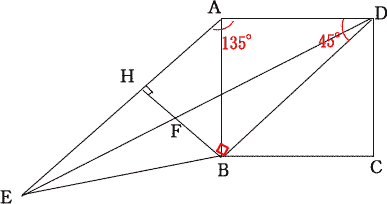
AH//DBより　台形AHBDにおいて、∠AHB = ∠HBD = 90°・・・① DBは正方形の対角線なので、∠BDA = 45°・・・② ①，②より∠DAH = 360°- (90°×2 - 45°) = 135° ∠EAB = ∠HAB = ∠DAH - ∠DAB = 135°- 90°= 45°

答　　45°

(2)　解答

(2)線分BHの長さは[⑰]である。
解答
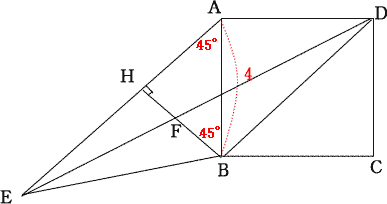
∠HAB = 45°，∠AAB = 90°より△AHBは直角二等辺三角形。線分BHの長さをχとすると、直角二等辺三角形の辺の比より

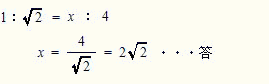
(3)　解答

(3)∠AEBの大きさは[⑱]度である。
解答
△BEHにおいて、
直角二等辺三角形の辺の比より

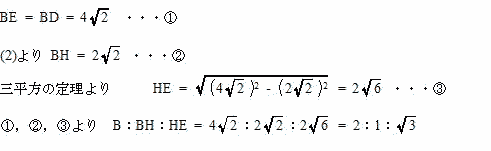したがって、直角三角形の辺の比より∠AEB = 30°

答　　　30°

(4)　解答

(4)　三角形AEBの面積は[⑲]c㎡である。
解答

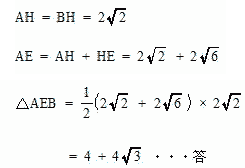(5)　解答

(5)三角形FEHと三角形FBDの面積の比を最も簡単な整数で表すと、(三角形FEH)：(三角形FDB) = [⑳]である。
解答
△FEHと△FBDにおいて ∠EHF = ∠DBF = 90° ∠HFE = ∠BFD (対頂角) 二角相等より△FEH　∽ △FBD

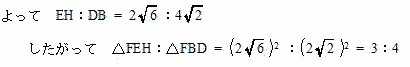答　　△FEH：△FBD = 3：4