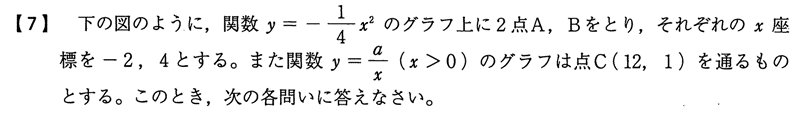プロ家庭教師集団スペースＯＮＥの高校受験志望校合格のための過去問対策沖縄県立高等学校2007年度数学入試問題円周率

沖縄県立高等学校過去問研究

関数のグラフは　高校入試対策では必修問題です。

今回取り上げた沖縄県２０１０年度の問題は比例・反比例・二次関数の総合問題です。（２）は（３）の誘導です。（３）は等席変形の基本問題です。

数学入試問題　　関数のグラフ

今回の沖縄県の関数のグラフ問題は、

スペースＯＮＥプロ家庭教師の解答で、沖縄県の発表ではありません。

問2　解説解答

２点Ａ，Ｂを通る直線の傾きを求めなさい。
解説
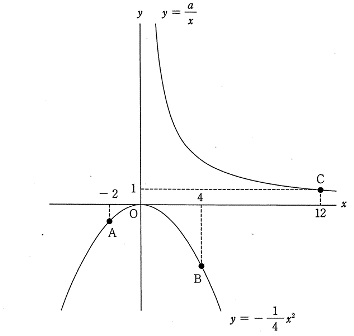
点Ａのｘ座標がー２なので、ｙ座標は　ｙ＝ー1/4×（ー２）2＝ー１点Ｂのｘ座標が４なので　ｙ座標は　ｙ＝ー1/4×（４）2＝ー４よって　点Ａ（－２，－１），Ｂ（４，－４）を通る直線の傾きは｛ー４－（－１）｝÷｛４－（－２）｝＝-1/2
答　　-1/2

(3)解説解答


解説
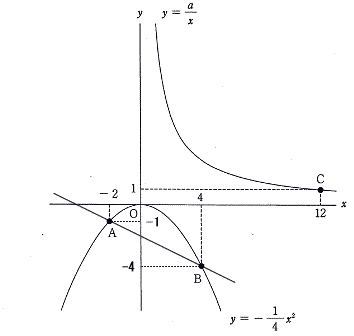
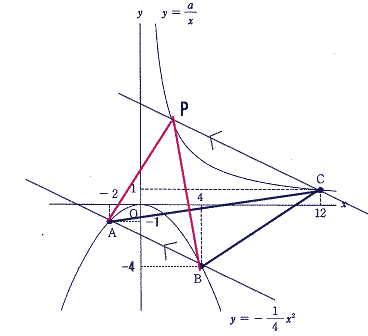
△ABFP＝△ABCのとき　AB//PCとなるので PCの傾きはABの傾きに等しい。直線ABの傾きは問２より　－1/2　なので点P,Cを通る直線の式は傾き-1/2,　点C( 12,1 )　を通る直線の式となる。よって　ｙ＝－1/2χ＋ｂに　χ＝１２,ｙ＝１を代入して　ｂ＝７　　　　y＝－1/2χ＋７点Pの座標は　直線　y＝－1/2χ＋７と　放物線ｙ＝12/χ　との交点になるので、－1/2χ＋７＝12/χ　　これを解いて χ＝２　　　χ＝１２（点Cのχ座標）より点Cのχ座標は２ｙ＝１２÷２＝６
答　　　（２,　６）

2010年度県立高校入試問題(過去問) 解答解説