
埼玉県立高等学校共通入試問題過去問研究
2015年度埼玉県立高校前期共通数学入試問題は 例年通り大問4題構成。1.小問集合11問 2.小問集合4問 3.平面上の点移動 4.図形の折り返し が出題されました。
試験時間は50分間。 例年通りスピードと正確さが求められる出題でした。
前期数学入試問題 3平面図形上の点移動

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


2015年度埼玉県立高校前期共通数学入試問題は 例年通り大問4題構成。1.小問集合11問 2.小問集合4問 3.平面上の点移動 4.図形の折り返し が出題されました。
試験時間は50分間。 例年通りスピードと正確さが求められる出題でした。
前期数学入試問題 3平面図形上の点移動
| (1) 点Pが点Dに向かっているとき、点Aを出発してからχ秒後の線分APの長さを、χを表しなさい。 |
| 解説 |
| 点PはAD間を5秒間で進むので、点Pの速さは 15÷5 = 3cm/秒 距離 = 速さ×時間 より 線分APの長さ= 3χ |
| 答 3χ |
 |
| 1回目解説(方程式で解く) |
| 点Qの速さは 15÷7.5 = 2(cm/秒) よって 点Bを出発してからχ秒後の線分BQの長さは 2χ 1回目に四角形ABQPの面積が長方形ABCDの面積の1/2となるのは、線分APと線分BQの和が15cmになるときなので、 3χ + 2χ = 15 より χ = 3 |
| 1回目別解説(平面図形で解く) |
| 点Qの速さは 15÷7.5 = 2(cm/秒)なので、点Pと点Qの距離の比は3:2 |
| 1回目に四角形ABQPの面積が長方形ABCDの面積の1/2となるのは下図の通り |
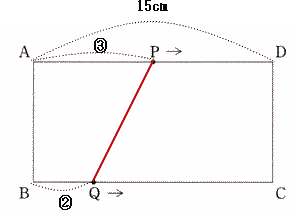 |
| ③+② = ⑤ = 15cmになるとき、 |
| したがって、③ = 9cm 点Pの速さは秒速3cmなので、 9÷3 = 3 |
| 2回目解説(方程式で解く) |
| 2回目に四角形ABQPの面積が長方形ABCDの面積の1/2となるのは点Qが点Cを折り返してから、点Pが点Aに着くまでの間。 |
| 点Qが点Cに着くのはグラフより出発後7.5秒後。このとき点PはPD間2.5×3 = 7.5cm。 |
| 2回目は線分ADと線分QCの和が15cmになるときなので、点Pと点Qが合わせて15 - 7.5 = 7.5cm進んだときに四角形ABQPの面積が長方形ABCDの面積の1/2となる。 |
| したがって 3χ + 2χ = 7.5 より χ = 1.5 7.5 + 1.5 = 9 |
| 答 1回目 3秒後 2回目 9秒後 |