高校受験指導専門プロ家庭教師の過去問研究

西南女学院高等学校受験指導はスペースＯＮＥ福岡校のプロ家庭教師にお任せください。

	ご依頼専用ダイヤル	0120-604-405
	お問い合わせ(本部・東京)	03-6868-6040
	お問い合わせ(福岡校)	093-592-6658
	お問い合わせメール
	ws-spaceone

プロ家庭教師集団スペースONE

HOME

2015年度西南女学院高等学校数学入試問題解答解説

西南女学院高等学校過去問研究

2015年度西南女学院高等学校の数学入試問題は　例年通りの出題構成で、１．小問集合　２．割合　３．立体図形(含証明問題)　４．関数のグラフ　５．立体図形　大問５題の出題でした。

１．は解答のみを解答欄に書く形式で、２～５．は途中式を書く解答形式でした。

今回は　スペースONE福岡校のプロ家庭教師が　3. 立体図形を解説します。　

問題

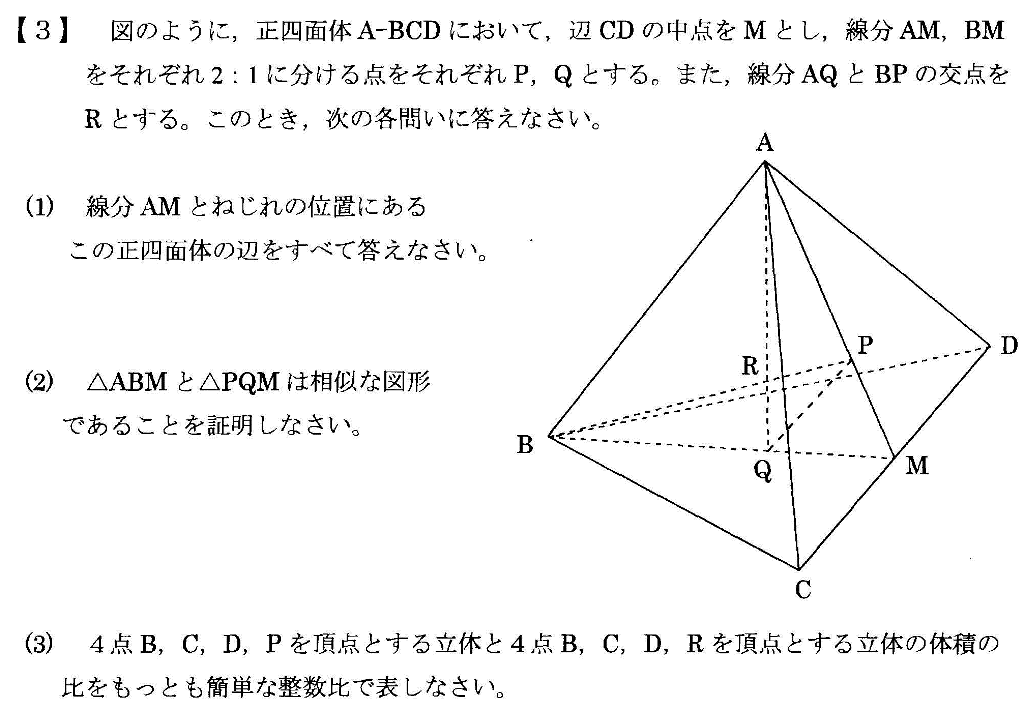スペースＯＮＥプロ家庭教師の解答で、西南女学院高等学校の発表ではありません。

　
(1)　解説

(1)　線分AMとねじれの位置にあるこの正四面体の辺をすべて答えなさい。
解説解答
ねじれの位置は空間における2直線の位置関係で「平行でなく」、「交わりもしない」場合なので、2直線が同一平面上にないことです。注意しなければならないのは同一平面上にあって、辺を延長すると交わる場合も、2直線が交わるという位置関係になることです。
線分AMと平行な辺は0，線分AMと交わる辺は　AB，AC，AD，CD よって　ねじれの位置にある辺は　BC，BD
答　　　辺BC，辺BD

(2)　解説

(2)　△ABMと△PQMは相似な図形であることを証明しなさい。
解説
△ABMと△PQMにおいて、仮定より　MP：PA = PQ：QB = 1：2より　PQ//AB したがって　∠ABM = ∠PQM (平行線の同位角) ∠BMA = ∠MAB (共通) 二角相等より　△ABM ∽ △PQM

(3)　解説

(3)　4点B, C, D, Pを頂点とする立体と4点B, C, D, Rを頂点とする立体の体積の比をもっとも簡単な整数の比で表しなさい。
解説
4点B, C, D, Pを頂点とする立体と4点B, C, D, Rを頂点とする立体は、ともに△BCDを底面にする三角錐なので、高さの比が体積の比になる。，
PQ//AB　より　MP：PA = 1：2 なので、PQ：AB = 1：3 また　△PQR ∽ △BAR より　BR：BP 点Ｒから△BCDに垂線を下ろしその公点をR'，点Pから△BCDに垂線を下ろしその公点をP'とする。 △BPP'∽ △BRRP' より　PP'：RR' = 4：3 したがって　三角錐P -BCDの高さと三角錐R-BCDの高さの比が4：3なので、三角錐P -BCDの体積と三角錐R-BCDの体積比も　4：3

答　　　4：3

ＴＯＰに戻る

高等学校受験過去問研究

プロ家庭教師集団スペースＯＮＥリンク集

大学受験過去問研究

医大医学部受験過去問研究

志望校合格のための医大・医学部入試情報

中学受験過去問研究

志望校合格のための中学入試情報

Copyright(c)2007All Rights Rserved.

このホームページのすべての文章の文責および著作権はプロ家庭教師集団SPACE ONEに属します。