高校受験指導専門プロ家庭教師の過去問研究
西南女学院高等学校受験指導はスペースONE福岡校のプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(本部・東京) |
03-6868-6040 |
|
お問い合わせ(福岡校) |
093-592-6658 |
 |
お問い合わせメール |
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
 HOME
HOME
2015年度西南女学院高等学校数学入試問題解答解説
西南女学院高等学校過去問研究
2015年度西南女学院高等学校の数学入試問題は 例年通りの出題構成で、1.小問集合 2.割合 3.立体図形(含証明問題) 4.関数のグラフ 5.立体図形 大問5題の出題でした。
1.は解答のみを解答欄に書く形式で、2〜5.は途中式を書く解答形式でした。
今回は スペースONE福岡校のプロ家庭教師が 4. 関数のグラフを解説します。
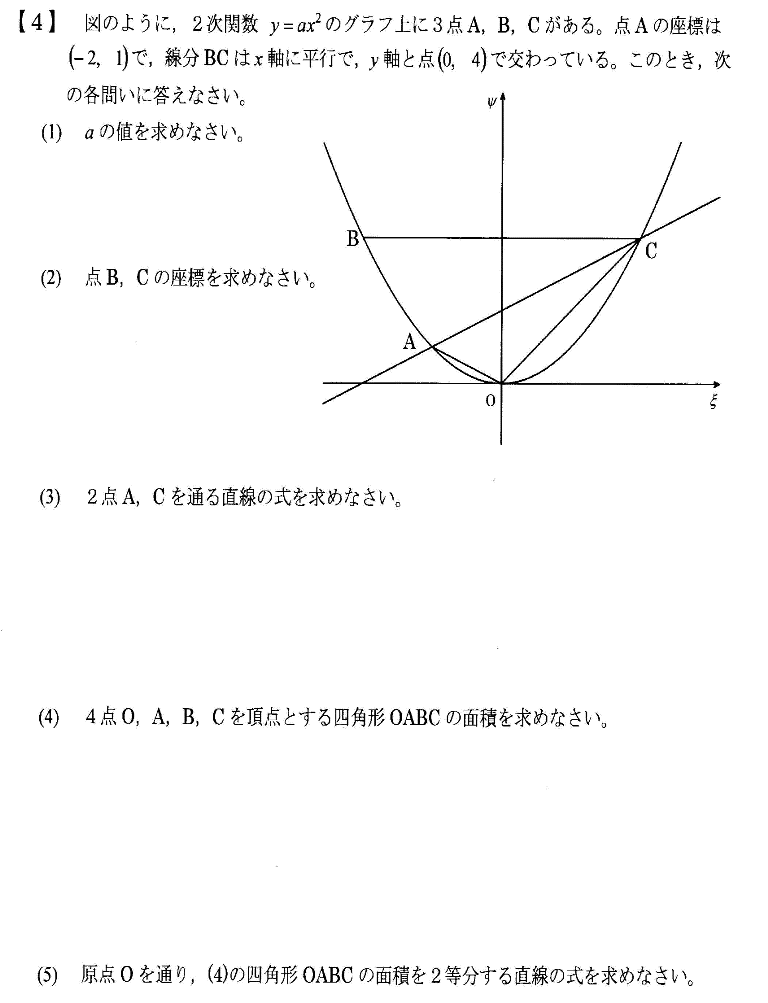
問題
スペースONEプロ家庭教師の解答で、西南女学院高等学校の発表ではありません。
(1) 解説
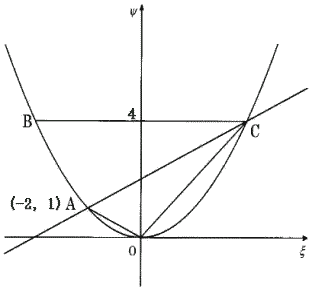
| (1) aの値を求めなさい。 |
|
| 解説解答 |
|
 |
 |
|
|
|
|
(2) 解説
| (2) 点B,Cの座標を求めなさい。 |
| 解説 |
|
、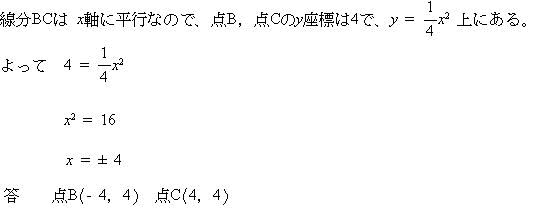 |
 |
|
|
|
|
(3) 解説
| (3) 2点A,Cを通る直線の式を求めなさい。 |
| 解説 |
|
 |
 |
|
|
(4) 解説
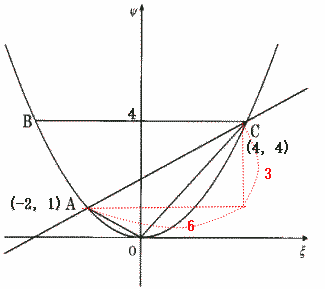
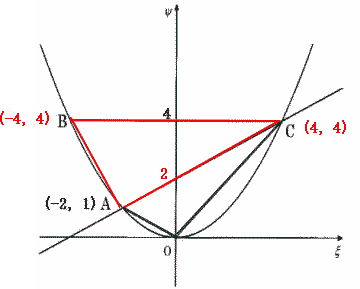
| (4) 4点O,A,B,Cを頂点とする四角形OABCの面積を求めなさい。 |
| 解説 |
|
四角形OABC = △BAC + △AOC
△BACの面積 = 点B,点Cのχ座標の差 × 点Bと点Aのy座標の差÷2 なので
△BACの面積 = {4 - ( - 4)}× ( 4 - 1)÷2 = 12
△AOCの面積は 直線ACの切片が2なので、
△AOCの面積 = 点A,点Cのχ座標の差 × 2 ÷2 なので
△AOCの面積 = {4 - ( - 2)}×2÷2 = 6
四角形OABCの面積 = 12 + 6 = 18
答 18 |
 |
|
|
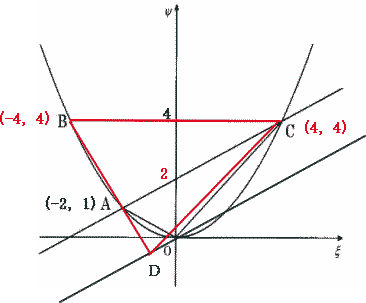
| 別解 等積変形で求める |
|
直線ACと平行で原点Oを通る直線と直線BAとの延長上の直線との交点をDとする。
△AOCの面積と△ADCの面積は等しいので、
四角形OABCの面積 = △BACの面積 + △AOCの面積 = = △BACの面積 + △ADCの面積 = △BDCの面積

|
 |
|
|
(3) 解説
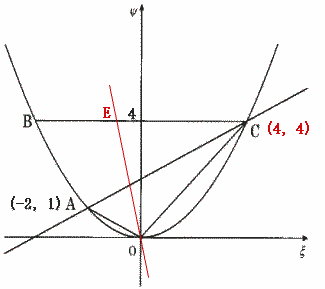
| (5) 原点Oを通り、(4)の四角形OABCの面積を2等分する直線の式を求めなさい。 |
| 解説 |
|
直線BC上に四角形OABCの面積を2等分する点をEとする。
△EOC = 18÷2 = 9
△EOCの高さは4なので、点Eと点Cのχ座標の差は
 |
 |
|
|
HOME
Copyright(c)2007All Rights Rserved.
このホームページのすべての文章の文責および著作権はプロ家庭教師集団SPACE ONEに属します。