高校受験指導専門プロ家庭教師の過去問研究

西南女学院高等学校受験指導はスペースＯＮＥ福岡校のプロ家庭教師にお任せください。

	ご依頼専用ダイヤル	0120-604-405
	お問い合わせ(本部・東京)	03-6868-6040
	お問い合わせ(福岡校)	093-592-6658
	お問い合わせメール
	ws-spaceone

プロ家庭教師集団スペースONE

HOME

2015年度西南女学院高等学校数学入試問題解答解説

西南女学院高等学校過去問研究

問題

スペースＯＮＥプロ家庭教師の解答で、西南女学院高等学校の発表ではありません。

　
(1)　解説

(1)　(1)　AD = CEであることを証明しなさい。 解説解答 △ABDと△CBEにおいて、過程より AB = CB, BD = BE,　∠ABD = ∠DBE = 60° 二辺とその間の角がそれぞれ等しいので　△ABD　≡　△CBE したがって　AD = CE

(2)　解説

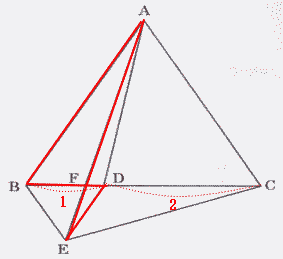
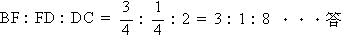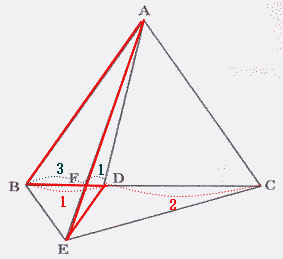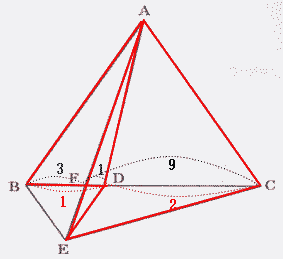
(2)　BD：DC = 1：2とするとき �@　次の線分の比をもっとも簡単な整数の比で答えなさい。 (ア) 　AF：FE 解説 △FABと△FEDにおいて、 ∠BFA = ∠DFE (対頂角) ∠ABF = ∠EDF = 60° 二角相等なので　△FAB ∽ △FED よって　FA：FE = AB：ED BD：DC = 1：2なので　AB：ED = BD + DC：BD = 1 + 2：1 = 3：1 したがって　AF：FE = 3：1 答　　3：1 (イ) 　ＢＦ：ＦＤ：ＤＣ 解説 (ア) △FAB ∽ △FEDより　ＢＦ：ＤＦ = ３：１ BD：DC = 1：2なので �A　四角形ABECの面積は△ADEの面積の何倍かを求めなさい。 解説 △AEDと△AECは底辺AEが共通なので、高さの比 = 面積比になるから ＦＤ：ＦＣ = 1：1 + 8 = 1：9 よって　△AED：△AEC = 1：9 ・・・�@ また△AEDと△ABEは底辺AEが共通なので、高さの比 = 面積比になるから ＦＤ：ＦB = 1：3 よって　△AED：△ABE = 1：3　・・・�A �@，�Aより △AED：△AEC：△ABE = 1：9：3 △AED：四角形ABEC = △AED：△AEC + △ABE = 1：9 + 3 = 1 ： 12 したがって四角形ABECの面積は△ADEの面積の12倍 答　　12倍

ＴＯＰに戻る

高等学校受験過去問研究

プロ家庭教師集団スペースＯＮＥリンク集

大学受験過去問研究

医大医学部受験過去問研究

志望校合格のための医大・医学部入試情報

中学受験過去問研究

志望校合格のための中学入試情報

HOME

Copyright(c)2007All Rights Rserved.

このホームページのすべての文章の文責および著作権はプロ家庭教師集団SPACE ONEに属します。