���Z�w�����v���ƒ닳�t�̐ō����w�Z�ߋ��⌤��
�ō����w�Z�w���̓X�y�[�X�n�m�d�̃v���ƒ닳�t�ɂ��C�����������B
 |
���˗���p�_�C���� |
0120-604-405 |
| ���₢���킹(�{���E����) |
03-6868-6040 |
|
���₢���킹(�����Z) |
093-592-6658 |
 |
���₢���킹���[�� |
|
 |
ws-spaceone |
|
�v���ƒ닳�t�W�c�X�y�[�XONE
 HOME
HOME
2010�N�x�ō����w�Z�������(�ߋ���) ���
�ō����w�Z�ߋ��⌤��
2010�N�x�ō����w�Z���w�������́@��N�ʂ�@�v�Z�C����W���C���R��̖��\���ŁA�o����e�́@�P�D�`�S�D�l���v�Z�E���������@�T�D����W���@�U�D�ꎟ���ƃO���t�@�V�D���̐}�`�@�W�D�ꎟ���Ɠ��̃O���t�ł����B
���w�������͋��ȏ��̉��K��背�x���Ȃ̂ŁA��Ƃ��Ă͋��ȏ��̖������S�Ƀ}�X�^�[���邽�߁A���w�R�N�Ԃ̋��ȏ��̑����K�����ċ������������邱�Ƃł��B
����́@�T�D����W����������܂��B
���T
�X�y�[�X�n�m�d�v���ƒ닳�t�̉ŁA�ō����w�Z�̔��\�ł͂���܂���B
(1) �����
| �i�P�j�@�R�_�`�i�Q�C�[�R�j�C�@�a�i�[�S�C�|�Q�j�C�o�i�U�C�R�j������B�_�o��ʂ�X�����̒����Ɛ����`�a������邽�߂̂��͈̔͂����߂�B |
| ��� |
|
|
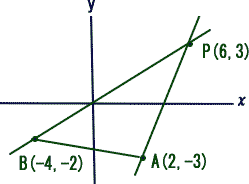 |
| �_�o��ʂ钼�����_�a��ʂ�Ƃ��̌X���́@�����i�R�{�Q�j���i�U�{�S�j��1/2 |
| �_�o��ʂ钼�����_A��ʂ�Ƃ��̌X���́@�����i�R�{�R�j���i�U�|�Q�j��3/2 |
| ����ā@���̒l�͈̔͂́@�@1/2������3/2 |
|
|
| ���@�@�@�@�@1/2������3/2 |
|
|
|
(2)�����
| (2)�@���͂̒������S�S�����̒����`������B���̒����`�̏c�̒������W���������A���̒������U�����Z�����������`�̖ʐς́A���Ƃ̒����`�̖ʐς����P�Q���u�������B���̂Ƃ��A���Ƃ̒����`�̖ʐς����߂�B |
|
|
|
| ��� |
|
|
|
| �c�̒����Ɖ��̒����̘a�́@�S�S���Q���Q�Q�@�c�̒������ԂƂ���ƁA���̒����͂Q�Q�|�� |
|
|
|
| ���Ƃ̒����̖ʐς́@ �ԁi�Q�Q�|�ԁj���|��2�{�Q�Q�� |
|
|
|
| �c�̒������W���������A���̒������U�����Z�����������`�̖ʐς́@�i�ԁ{�W�j�~�i�Q�Q�|�ԁ|�U�j���[��2�{8�ԁ{128 |
|
|
|
| ����ā@�@�|��2�{22�ԁ[�i�[��2�{8�ԁ{128�j��12�@�@�@�@����������ăԁ�10cm�E�E�E�c�̒��� �@�@�@���̒����́@22�|10=12cm |
|
|
|
| ���Ƃ̒����`�̖ʐς́@10�~12��120 |
|
|
|
|
|
|
|
| ���@�@�@�@120c�u |
|
|
|
|
|
(3)�����
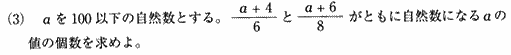 |
| ��� |
| (a+4)/6���`�C�@(a+6)/8���a�Ƃ����B |
| (a+4)/6���`�@�@���@�@a���U�`�[�S�@�@�@�F�i�S�{�Q���U�j |
| �@(a+6)/8���a�@�@���@�@a���W�a�[�U�@�@�@�F�i�U�{�Q���W�j |
| ����ā@�@a�́@�U�ƂW�̌��{�����Q�傫�����ɂȂ�B�@�@�U�ƂW�̍ŏ����{���́@�Q�S |
| �P�O�O�ȉ��̎��R���Ł@�@a�ɓ��Ă͂܂鐔�́@�@�Q�C�@�Q�U�C�T�O�C�V�S�C�X�W�@ |
|
| ���@�@�@�T�� |
|
|
(4)�����
| ����������P���āA�o���ڈȊO�̂T�̖ڂ̘a�����_�ɂȂ�Q�[��������B���̃Q�[�����R�l�ōs�����Ƃ��A�R�l�̓��_�̍��v���T�V�_�ȏ�ɂȂ�m�������߂�B |
| ��� |
| �P����U�Ԃł̖ڂ̐��̍��v�́i�P�{�U�j�~�U���Q���Q�P |
| �R�l�̃T�C�R���̖ڂ̍��v�͂U�R |
| �R�l�̓��_�̍��v���T�V�_�ȏ�ɂȂ�̂́@�R�l�̏o���T�C�R���̖ڂ̍��v���@�U�R�|�T�V���U�ȉ��ɂȂ�ꍇ�ɂȂ�B |
�R�l�̃T�C�R���̖ڂ��i�P�C�P�C�P�j�@�P�ʂ�@�i�P�C�P�C�Q�j�̂Ƃ��@�R�ʂ�@�@�i�P�C�Q�C�Q�j�@�R�ʂ�@�@�i�Q�C�Q�C�Q�j�@�P�ʂ�@�@
�i�P�C�P�C�R�j�@�R�ʂ�@�@�i�P�C�Q�C�R�j�@�U�ʂ�@�@�i�P�C�P�C�S�j�@�R�ʂ�@�@�v�@�Q�O�ʂ�@�@
�R�l�̖ڂ̏o���͑S���Ł@�U�~�U�~�U�ʂ肠��̂ŁA�@�m���́@�@�Q�O���i�U�~�U�~�U�j���T�^�T�S |
|
| ���@�@�@�@�@�@�@�T�^�T�S |
|
|
(5)�����
 |
|
|
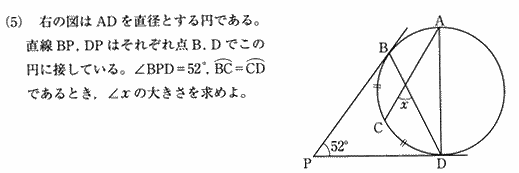
| ��� |
|
|
�~�̒��S���n�Ƃ���B
��ADP = ��90���E�E�E�i�~�̐ڐ��͐ړ_��ʂ锼�a�ɐ����j
��BDP����CBP���i�P�W�O�|�T�Q�j���Q���U�S��
��ADB���X�O�|�U�S���Q�U��
��BOD�ɂ����ā@BO��DO�i�~O�̔��a�j
��BOD���P�W�O�|�Q�U�~�Q���P�Q�W��
��BC����CD�Ȃ̂Ł@�@��BOC����DOC���P�Q�W���Q���U�S��
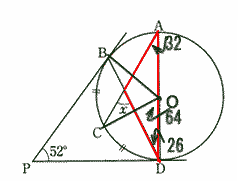
���S�p�Ɖ~���p�̊W���
��CAD��1/2��COD���P�Q�W���Q���Q���R�Q
�ڃԁ���CAO�{��BDO=�Q�U�{�R�Q���T�W�� |
 |
|
|
|
|
|
|
| ���@�@�@�T�W�� |
|
|
|
|
|
|
|
|
|
HOME
Copyright(c)2007All Rights Rserved.
���̃z�[���y�[�W�̂��ׂĂ̕��͂̕��ӂ���ђ��쌠�̓v���ƒ닳�t�W�cSPACE ONE�ɑ����܂��B


