有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

専修大学付属高校　過去問対策

専修大学付属高等学校過去問研究

専修大学付属高等学校の2020年度一般入試は　募集人数男子110名　女子90名に対し　応募者男子286名　女子282名　受験者男子283名　女子281名　合格者男子123名　女子153名でした。

数学入試問題は問1.小問集合７問、問2.関数のグラフ　問3.方程式の応用　問4.座標平面　問5.統計　問6.平面図形内の点移動　が出題されました。

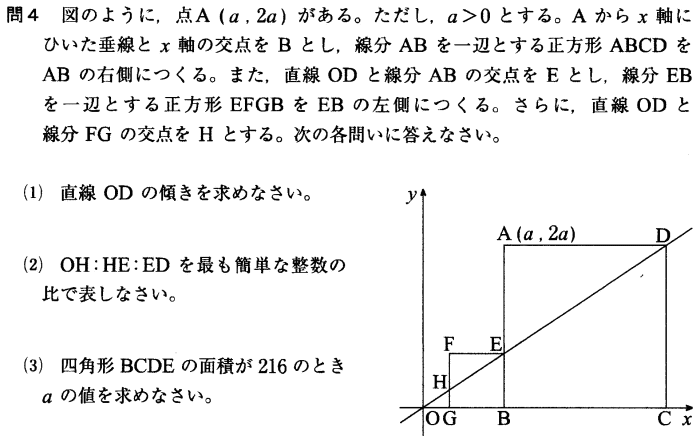
今回は　4.座標平面を解説します。相似比を用いた出題です。正方形の性質を理解したうえで解きましょう。

専修大学附属高校数学入試問題　2020年度入試問題　問4．座標平面　問題


専修大学附属高校数学入試問題　2020年度入試問題　問4．座標平面(1)　解説解答

(1)　直線ODの傾きを求めなさい。

解説解答



A(a，2a)であり、かつ四角形ABCDは正方形なので、AB = BC = CD = 2a，

点Bのx座標はaなので、点Cの座標は(a + 2a，0)，よって　点Dの座標は(3a，2a)

よって　直線ODの傾きは


専修大学附属高校数学入試問題　2020年度入試問題　問4．座標平面(2)　解説解答


(2)　OH：HE：EDをもっとも簡単な整数の比で表しなさい。

解説解答



FG // EB // DC　なので　△OHG　∽　△OEB　∽　△ODC

よって　OH：HE：ED = OG：GB：BC

(1)　より　OC：DC = [3]：[2]，BC = DC　なので、OB：BC = [3] - [2]：[2] = [1]：[2]

また　OB：EB = ③：②，GB = EB なので、OG：GB = ③ - ②：② = ①：②　

以上より　OB：BC = [1]：[2]，OG：GB = ①：②





専修大学附属高校数学入試問題　2020年度入試問題　問4．座標平面(3)　解説解答

Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com