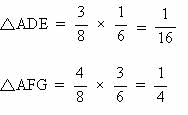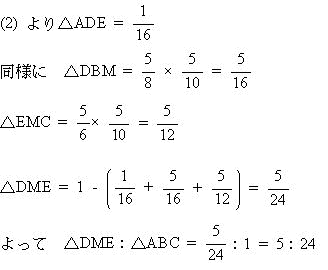立教新座高等学校過去問研究
2013年度立教新座高等学校入試結果は、志望者数 1,101名 受験者数1,088名 合格者553名 補欠者数 166名 補欠繰り上げ数63名 実質倍率 2.41倍でした。
立教新座高等学校の2013年度数学入試問題は小問集合4問、大問5題構成でした。出題内容は 2.整数の性質と因数分解,3.平面図形 4.確率 5.関数と図形 6.立体図形(空間図形の切断)でした。立教新座高校の数学は、問題によって難易度に差が大きいのが特徴です。
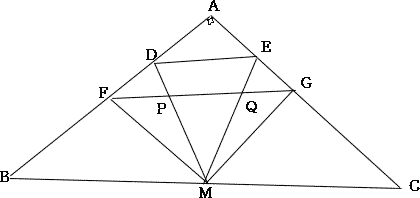
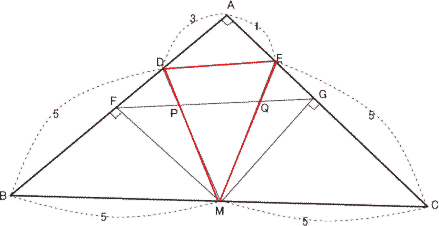
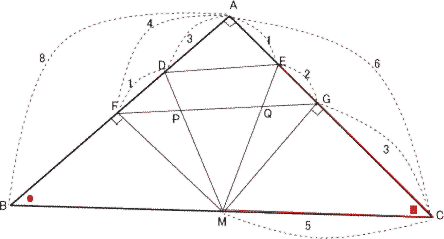
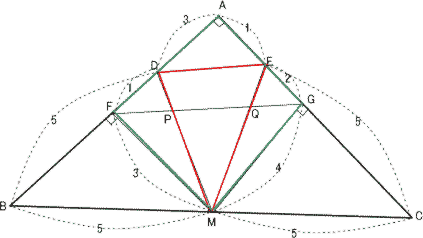
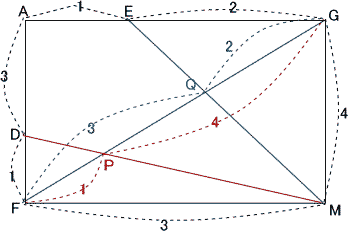
今回は 3.平面図形を解説します。 (1)(2)は相似比を用いた基本問題、(3)(4)は標準レベルの問題です。
立教新座高等学校の2013年度数学入試問題は小問集合4問、大問5題構成でした。出題内容は 2.整数の性質と因数分解,3.平面図形 4.確率 5.関数と図形 6.立体図形(空間図形の切断)でした。立教新座高校の数学は、問題によって難易度に差が大きいのが特徴です。
今回は 3.平面図形を解説します。 (1)(2)は相似比を用いた基本問題、(3)(4)は標準レベルの問題です。