
巣鴨高校 過去問対策


プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00



| (1) この3つが、直角二等辺三角形の内角の大きさとなる確率を求めよ。 |
| 解説 |
| 直角二等辺三角形の内角の大きさは 90°,45°,45° |
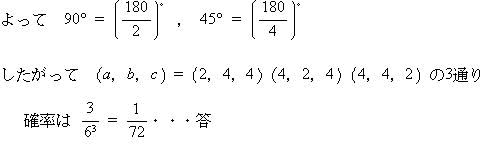 |
| (2) この3つが、辺の長さがすべて異なる三角形の内角の大きさとなる確率を求めよ。 |
| 解説 |
| サイコロの目の数1~6のときの角度は |
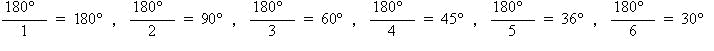 |
| よって 90°,60°,45°,36°,30°の組合せで、辺の長さが異なる三角形の組合せは、90°,60°,30°の場合のみなので、 a,b,cが(2,3,6)になるときの場合の数は 3×2×1 = 6通り |
| (3) この3つが、三角形の内角の大きさとなる確率を求めよ。 |
| 解説 |
| 直角二等辺三角形の内角の大きさとなる場合の数は 3通り。 辺の長さがすべて異なる三角形の内角の大きさとなる場合の数は 6通り。 辺の長さが全て同じとなる場合は (60°,60°,60°)となる場合なので、(3,3,3)の1通り 全部で10通りなので、 |