高校受験指導専門プロ家庭教師の駿台甲府高等学校過去問研究
駿台甲府高等学校受験指導はスペースONEのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(本部・東京) |
03-6868-6040 |
|
お問い合わせ(福岡校) |
093-592-6658 |
 |
お問い合わせメール |
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
 HOME
HOME
2009年度 駿台甲府高等学校入試問題(過去問) 解答解説
駿台甲府高等学校過去問研究
駿台甲府高等学校2009年度数学入試問題は Ⅰ計算小問集合11問 Ⅱ場合の数 Ⅲ一次関数 Ⅳ立体図形 の大問4題構成でした。
問題
スペースONEプロ家庭教師の解答で、駿台甲府高等学校の発表ではありません。
(1) 解説解答
| a = b のとき、mの値を求めよ。 |
|
|
|
| 解説 |
|
|
|
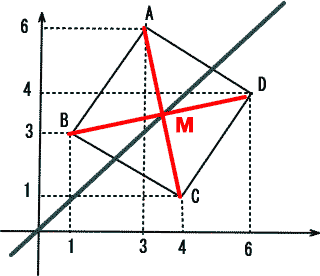
正方形ABCDの対角線の中心を通る直線で面積を二等分するので、
B(1,3),D(6,4)を結ぶ直線の中点Mの座標は
x=(1+6)÷2, y=(3+4)÷2
原点と(7/2 , 7/2)を通る直線の式は y=x
よって m=1 |
 |
|
|
| 答 1 |
|
|
|
|
|
(2)解説解答
| m = 3./2のとき a : b を最も簡単な整数の比で表せ。 |
|
| 解説 |
|
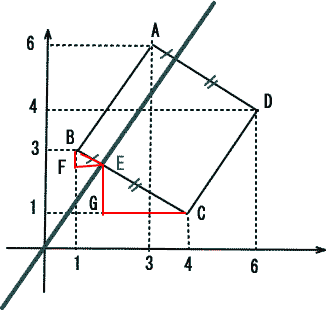
右図の通り ABの直線の傾きは 3/2 よって y=3/2と平行な直線になる。
y = 3/2 と直線BCの交点をEとすると BE:ECの辺の比が面積比 a : bとなる。
右図の通り △BFG∞△EGC よって BE:EC=BF:EG
直線BCの式は 傾き -2/3 切片 11/3 なので y=-2/3+11/3
y = 3/2 の直線との交点Eは(22/13 , 33/13)
BF=3-33/13=6/13 EG=33/13ー1=20/13
よって BF:EG=3:10 |
 |
| 答 3:10 |
|
|
|
(3)解説解答
| a : b = 2 : 1となるとき、mの値を求めよ。 |
|
| 解説 |
|
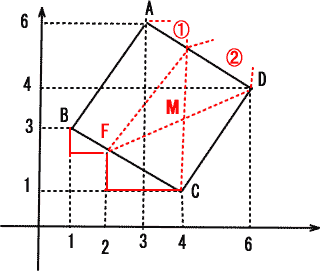
BCを1:2に分ける点をFとすると、Fのx座標は2なので
BCの直線の式 y=- 2/3 x+ 11/3に代入して、 y=7/3
図のように FDの中点を通る直線の式が a : b = 2 : 1 の条件を満たす。
FDの中点はF(2, 11/3) D(6,4)なので
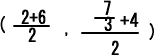
より (4, 19/6)
y=mxに(4, 19/6)を代入して
m=19/24
|
 |
| 答 19/24 |
|
|
|
HOME
Copyright(c)2007All Rights Rserved.
このホームページのすべての文章の文責および著作権はプロ家庭教師集団SPACE ONEに属します。