
栃木県立高等学校数学過去問研究
今回は 栃木県立高校数学入試問題4の平面図形問題2題を解説します。Ⅰは円の性質を用いた証明問題,2は三平方の性質を用いた基本的な問題です。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


今回は 栃木県立高校数学入試問題4の平面図形問題2題を解説します。Ⅰは円の性質を用いた証明問題,2は三平方の性質を用いた基本的な問題です。

| △ACD∽△ABEであることを証明しなさい。 |
| 解説 |
| 三角形の相似条件は ①3組の辺の比がすべて等しい。 ②2組の辺の比とその間の角がそれぞれ等しい。 ③2組の角がそれぞれ等しい。 のいずれかです。円の性質を用いた相似形の証明の場合 ③の2角相等で証明する問題が一般的です。 |
| 証明 |
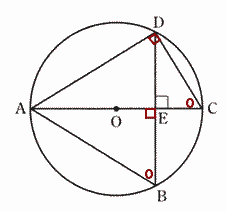 |
| △ACDと△ABEにおいて、 半円の弧に対する円周角なので、∠CDA = 90°,・・・① 仮定より ∠BEA = 90°・・・② ①,②より ∠CDA = ∠BEA ・・・③ 弧ADの円周角なので∠ACD = ∠ABE ・・・④ ③,④ より2角相等なので△ACD∽△ABE |
| (1) BCの長さを求めなさい。 |
| 解説 |
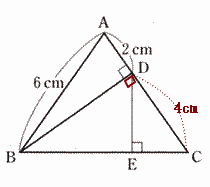 |
| △ABDと△CBDにおいて 三平方の定理より 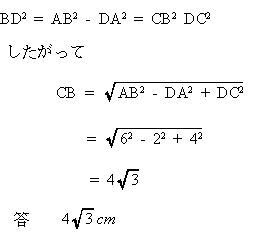 |
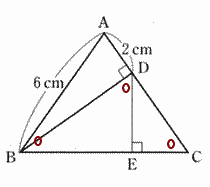
| (2) ∠BAC = a°とするとき、∠BDEの大きさをaを用いて表しなさい。 | |
| 解説 |
|
 |
|
| ∠EDA=∠BDA + ∠EDB ∠BDA = 90°なので ∠EDA = 90°+ ∠EDB 外角の性質より ∠EDA = 90°+ ∠EDB = ∠CED + ∠DCE ∠CED = 90°なので ∠EDA = 90°+ ∠EDB = 90°+ ∠DCE したがって ∠EDB = ∠DCE 二等辺三角形の底角の性質より |