
東京都立高等学校過去問研究
東京都立2009年度共通数学入試問題 1.小問集合抜粋

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


東京都立2009年度共通数学入試問題 1.小問集合抜粋
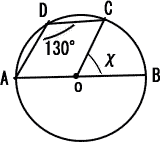

| 右図で、点Oは線分ABを直径とする円の中心で、2点C, Dは円Oの周上の点である。 ∠ADC=130°のとき、χで示した∠COBの大きさは何度か。 |
 |