���Z�w�����v���ƒ닳�t�̓����s�������w�Z�ߋ��⌤��
�����s�������w�Z�w���̓X�y�[�X�n�m�d�̃v���ƒ닳�t�ɂ��C�����������B
 |
���˗���p�_�C���� |
0120-604-405 |
| ���₢���킹(�{���E����) |
03-6868-6040 |
|
���₢���킹(�����Z) |
093-592-6658 |
 |
���₢���킹���[�� |
|
 |
ws-spaceone |
|
�v���ƒ닳�t�W�c�X�y�[�XONE
 HOME
HOME
2009�N�x�����s�������w�Z�������(�ߋ���) ���
�����s�������w�Z�ߋ��⌤��
���ʐ��w�������@�@���̃O���t
���R
 |
 |
 |
 |
 |
|
 |
 |
 |
|
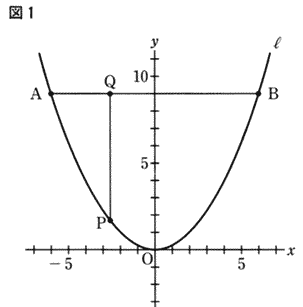
�E�̐}�P�ŁA�_O�͌��_�A�Ȑ� l �͊�y�� ��2�@�̃O���t��\���Ă���B ��2�@�̃O���t��\���Ă���B
�_A,�@�_B�͂Ƃ��ɋȐ� l ��ɂ���A���W�͂��Ƃ̂ꂼ��i�|�U�C�X�j�C�i�U�C�X�j�ł���B�_A�Ɠ_B�����ԁB
�Ȑ� l ��ɂ���A�����W���[�U���傫���U��菬�������ł���_��P�Ƃ���B
�_P��ʂ������ɕ��s�ȋȐ�����������AB�Ƃ̌�_��Q�Ƃ���B
���W���̂P�ڐ�����P�����Ƃ��āA���̊e��ɓ�����B
�m��P�n�@�_P�������W��a,����PQ�̒�����b�����Ƃ���Ba�̂Ƃ�l�͈̔͂��@
�@�@�|�S�� a ���R�@�@�̂Ƃ� b�̂Ƃ�l�͈̔͂�s�������g���ĕ\���B |
 |
|
|
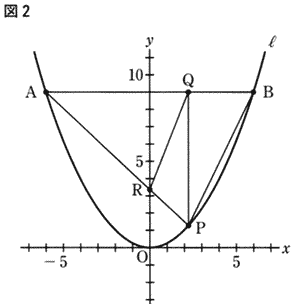
[��Q]�@�}�Q�́A�}�P�ɂ����āA�_P�̃ԍ��W�����̂Ƃ��A�_A�Ɠ_P�����сA����AP�Ƃ����Ƃ̌�_��R�Ƃ��A�_Q�Ɠ_R,�_B�Ɠ_P�����ꂼ�ꌋ�ꍇ��\���Ă���B
���̇@�C�A�ɓ�����B
�@�@�_R�̍��W���i�O�C�P�j�̂Ƃ��C�Q�_A�CP��ʂ钼���̎������߂�B
�A�@PQ=AQ�ƂȂ�Ƃ��C��PBA�̖ʐς̉����̂������B |
 |
|
|
|
 |
 |
 |
 |
t |
 |
 |
 |
 |
 |
�X�y�[�X�n�m�d�v���ƒ닳�t�̉ŁA�����s�������w�Z�̔��\�ł͂���܂���B
��P�@�����
��2�@�@�����
�@�@�_R�̍��W���i�O�C�P�j�̂Ƃ��C�Q�_A�CP��ʂ钼���̎������߂�B
|
��� |
|
|
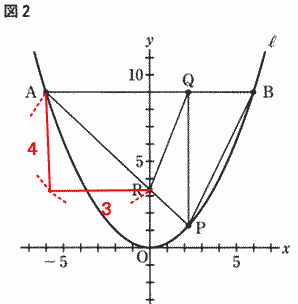 |
����AR�̌X���́@�O���t���@�|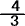
�ؕЂ́@R���W�i�O,�P�j���@�P�@
����ā@AP��ʂ钼���̎���
�����|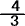 x�{�P x�{�P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
��2�@�A�����
�A�@PQ=AQ�ƂȂ�Ƃ��C��PBA�̖ʐς̉����̂������B
|
��� |
|
|
 |
PQ=AQ�ƂȂ�Ƃ��́@�_Q�C�_P�̂����W���@a�Ƃ���ƁA�_Q�̍��W�́ia�C�X�j�_P�̍��W�́ia�C�X�|a�|�U�j���ia�C�[a�{�R�j�@
�_P�͊��@y�� ��2�@��̓_�Ȃ̂ŁA ��2�@��̓_�Ȃ̂ŁA
���̎��Ɂia�C�[a�{�R�j��������
a2�{�Sa�|�P�Q���O�@ �ia�{�U�j�ia�|�Q�j���O�@
a���O���@a���Q�@Q�i�Q�C�X�j�@P�i�Q�C�Q�j
��RPQ�̖ʐρF��PBA�̖ʐρ��i�X�|�Q�j�~�Q���Q�F�U�~�Q�~�i�X�|�Q�j���Q���P�F�U�@�@
���@1/6
|
|
|
|
|
|
|
|
|
|
|
|
|
HOME
Copyright(c)2007All Rights Rserved.
���̃z�[���y�[�W�̂��ׂĂ̕��͂̕��ӂ���ђ��쌠�̓v���ƒ닳�t�W�cSPACE ONE�ɑ����܂��B

