東京都立高等学校数学過去問研究
2014年度都立高校数学入試問題は、例年通りの出題構成で、内容は１．小問集合９問(含作図) ２．場合の数と証明 ３．関数のグラフ ４．平面図形(含証明) ５．立体図形でした。
今回は 4．平面図形を解説します。
都立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
都立高校2014年度 数学入試問題 4. 平面図形 問題
都立高校2014年度 数学入試問題 4. 平面図形問１ 解説解答
| (問1) 図１において、∠BAPの大きさをa°とするとき、∠APQの大きさをaを用いた式で表せ。 |
| 解説 |
 |
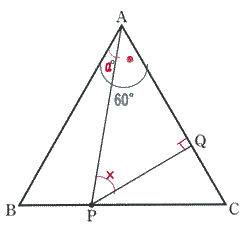| △ABCは正三角形なので ∠BAC = ∠BAP + ∠PAC = 60° よって ∠PAC = 60°- a° また △APQは直角三角形なので ∠PAQ + ∠APQ = 90° したがって ∠APQ = 90°- (60°- a°) = 30° + a° |
| 答 30° + a° |
都立高校2014年度 数学入試問題 4. 平面図形問２ 解説解答
| ① △PSR ∽ △ASQであることを証明せよ。 |
| 解答 |
 |
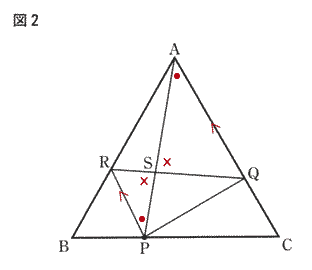| △PSR ∽ △ASQにおいて AC // RP(仮定)より ∠RPS = ∠QAS（平行線の錯角） ・・・① ∠PSR = ∠ASQ （対頂角） ・・・② ①，②より 二角相等なので△PSR ∽ △ASQ |
都立高校2014年度 数学入試問題 4. 平面図形問3 解説解答
| ② 図２において、 BP：PC = 1：2のとき、△PQSの面積は△ABCの面積の何分のいくつか。 |
| 解説 |
 |
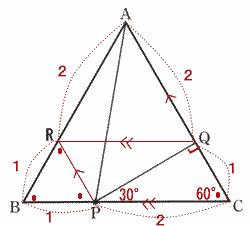| △ABPは正三角形なので 3辺の長さを それぞれAB = BC = CA = 3とする。 △RBPにおいて、 RP // AC より ∠RPB = ∠ACP = 60° よって △RBPは正三角形なので RB = BP = 1 より AR = 3 - 1 = 2 ・・・① また △QPCにおいて ∠CQP = 90°, ∠PCQ = 60°なので ∠QPC = 30° 三角形の辺の比 より PC ：CQ = 2：1 よって AQ = 3 - 1 = 2 ・・・② ①, ②より RQ // BC よって AS：SP = 2：1  |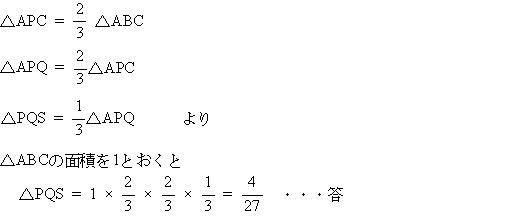
