東京都立高等学校数学過去問研究
2016年度都立高校数学入試問題は、例年通りの出題構成で、内容は１．小問集合９問(含作図) ２．文章題(数の性質) ３．関数のグラフ ４．平面図形(含証明) ５．立体図形でした。
今回は ４．平面図形(含証明)を解説します。 平面図形はそれぞれの図形の性質をよく理解して解いていきましょう。
都立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
都立高校2016年度 数学入試問題 4. 平面図形 （証明問題） 問題
問１ 解説解答
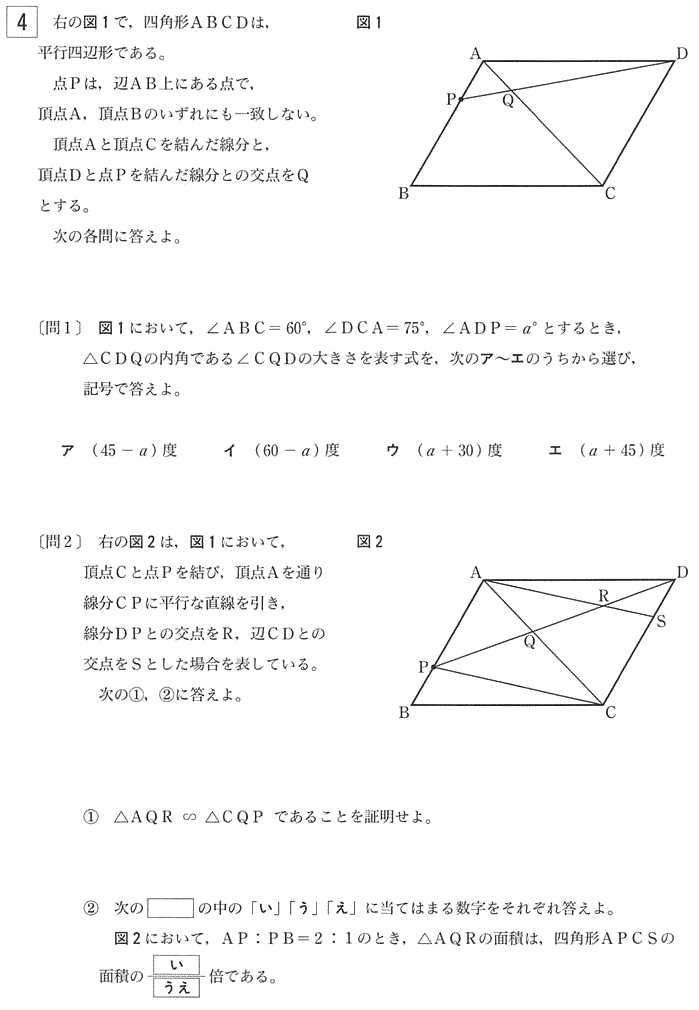
| (問1) 図1において、∠ABC = 60°，∠DCA = 75°，∠ADP = a°とするとき、△CDQの内角である∠CQDの大きさを表す式を、次のア～エのうちから選び、記号で答えよ。 ア (45- a)度 イ(60- a)度 ウ(a + 30)度 エ(a + 45)度 |
| 解説 |
 |
| 平行四辺形の性質より ∠ABC = ∠CDA = 60°， よって ∠CDQ = 60°- a°， ∠CQD = 180°- (75°+ 60°- a°) = 45°- a° |
| 答 ア |
問２ ① 解説解答
| 問2 ① △AQR ∽ △CQPであることを証明せよ。 |
| 証明 |
 |
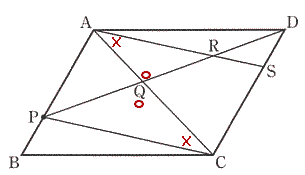| △AQRと△CQPにおいて 仮定より ∠RAQ = ∠PCQ (平行線の錯角)・・・① ∠AQR = ∠CQP (対頂角)・・・② ①，②より2組の角がそれぞれ等しいので △AQR ∽ △CQP |
問２ ② 解説解答
