
東京都立高等学校共通理科過去問研究
2017年度東京都立高等学校理科入試問題は、例年通りの大問6題構成、出題形式でした。
今回は 物体の運動を解説します。
実験の結果から読み取れる情報をもとに解いていきましょう。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


2017年度東京都立高等学校理科入試問題は、例年通りの大問6題構成、出題形式でした。
今回は 物体の運動を解説します。
実験の結果から読み取れる情報をもとに解いていきましょう。


| [問1] <実験1>と<結果1>から、小球Aと小球Bにそれぞれ働く重力の大きさの関係お、小球Aと小球Bがそれぞれ床に着く直前の速さの関係を組み合わせたものとして適切なのは、次のア~エのうちではどれか。 |
| 解説 |
| 小球Aと小球Bは質量が異なるので、重力の大きさは異なる。 小球Aも小球Bも移動するのにかかった時間も移動距離も等しいので、小球Aと小球Bがそれぞれ床に着く直前の速さの関係は等しい、 |
| 答 イ |
| 問2 図6の矢印は、斜面上にある小球Aに働く重力を表したものである。小球Aに働く重力の斜面に平行な分力と斜面に垂直な分力を、解答用紙の方眼を入れた図にそれぞれ矢印でかけ。 |
| 解説 |
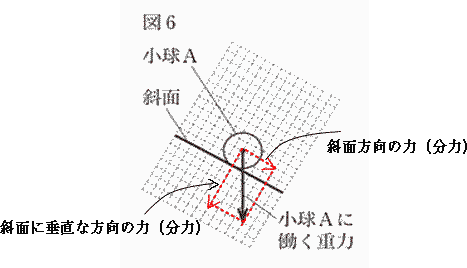 |
| 解答 |
 |
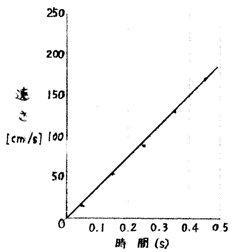
| 問3 <結果2>から、①から⑤までの各区間における小球Bの平均の速さを求め、解答用紙の方眼を入れた図に、各区間の中央の時間に●を用いて記入し、時間と速さのグラフをかけ。 |
| 解説 |
| 速さ = 移動した距離÷時間 なので、①区間の平均の速さは毎秒1.7cm,中央の時間は0.05秒,②区間の平均の速さは毎秒5.6cm,中央の時間は0.15秒,③区間の平均の速さは毎秒9.0cm,中央の時間は0.25秒,④区間の平均の速さは毎秒1372m,中央の時間は0.35秒,⑤区間の平均の速さは毎秒16.8cm,中央の時間は0.45秒, |
| 答 |
 |
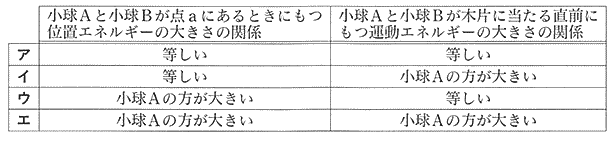
| 問4 <結果2>から、小球Aと小球Bが点aにあるときにもつ位置エネルギーの大きさの関係と、小球Aと小球Bが木片に当たる直前に持つ運動エネルギーの大きさの関係を組み合わせたものとして適切なのは、次の表のア~エのうちではどれか。 |
 |
| 解説 |
| 位置エネルギー[J] = 物体に働く重力[N] ×基準面からの高さ(m) 小球A,Bともに基準面からの高さは等しいので、位置エネルギーの大小は小球の質量(= 重力)によって決まる。 小球Aの移動距離 > 小球Bの移動距離 より 位置エネルギーは小球Aの方が大きい。 運動エネルギー[J] = 1/2 ×質量[kg] ×速さ×速さ 小球Aを当てた木片の移動距離の方が、小球Bを当てた木片の移動距離より長い。速さは移動距離に比例し、質量も小球Aの方が大きいので、小球Aの方が運動エネルギーが大きい。 |
| 答 エ |