東京都立新宿高等学校過去問研究
2011年度都立新宿高等学校独自数学入試問題は例年通り1.小問集合，２．関数のグラフ ３．平面図形 ４．立体図形の問題構成でした。
関数のグラフの問題は2010年の二次関数に代わって、2011年度は一次関数のグラフが出題されました。
関数のグラフの問題は2010年の二次関数に代わって、2011年度は一次関数のグラフが出題されました。
今回は２ 一次関数のグラフの問題を解説します。
東京都立新宿高校数学 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
東京都立新宿高校2011年度数学入試問題 2.一次関数のグラフ 問題
東京都立新宿高校2011年度数学入試問題 2.一次関数のグラフ(1) 解説解答
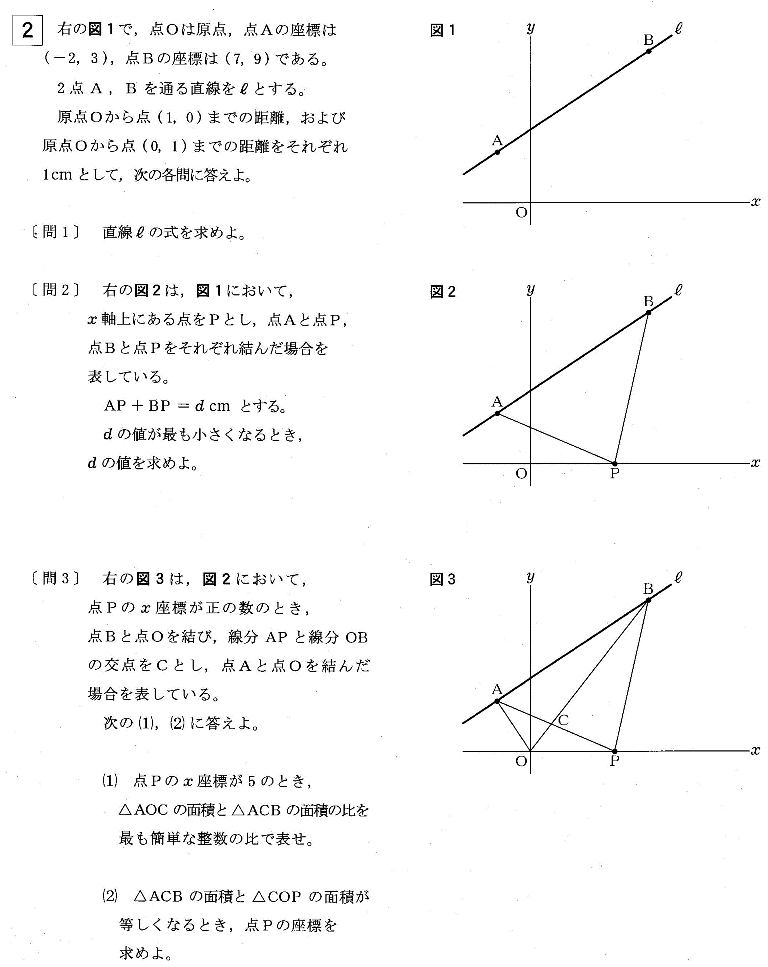
| (1) 直線ℓの式を求めよ。 |
| 解説 |
 |
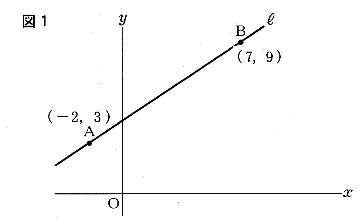| ２点 Ａ（-2,3） Ｂ(7,9)を通る直線の式なので |
 |
東京都立新宿高校2011年度数学入試問題 2.一次関数のグラフ(2) 解説解答
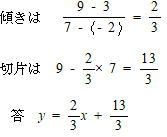| (2) 図２は、図１において、χ軸上にある点Pとし、点Aと点P，点Bと点Pをそれぞれ結んだ場合を表している。 AP + BP = d cmとする。 ｄの値が最も小さくなるとき、ｄの値を求めよ。 |
| 解説 |
 |
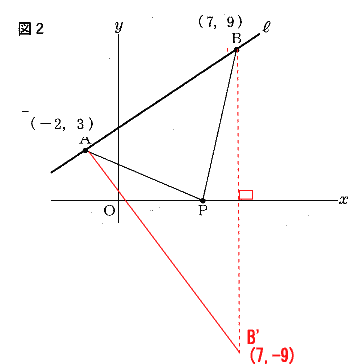| 点Bとχ軸に対称となる点B'をおく。 点B'の座標は （７，－９） 題意を満たすｄの値は 線分AB'となる。 三平方の定理より  ｄ＞０ より ｄ＝１５ |
| 答 １５ |
青山学院高等部数学入試問題6.平面図形(3) 解説解答
| (3) 図３は、図２において、点Pのχ座標が正の数のとき、点Bと点Oを結んだ場合を表している。 |
 |
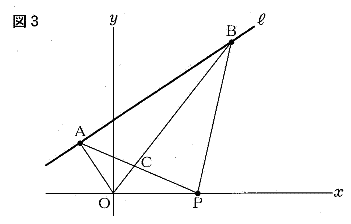| 次の（１）（２）に答えよ。 |
| （１） 点Pのχ座標が５のとき、△AOCの面積と△ACBの面積の比を最も簡単な整数の比で表せ。 |
| 解説 |
 |
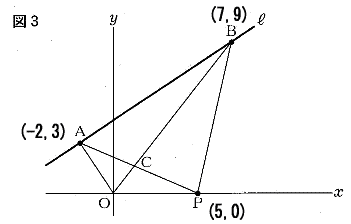| △AOCと△ACBは高さの等しい三角形なので、底辺の比＝面積比。 よって OC：CBを求めるとよい。 点Cは直線OBと直線APの交点なので |
 |
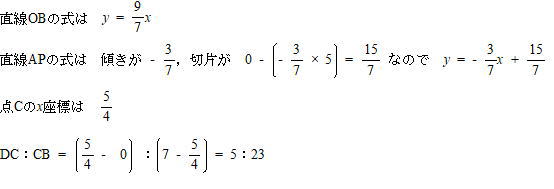| 答 ５：２３ |
| (2) △ACBの面積と△COPの面積が等しくなるとき、点Pの座標を求めよ。 |
| 解説 |
 |
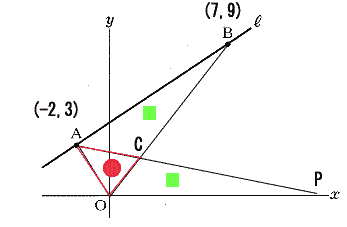| △AOCを共通とする三角形を考える。 △ACB＝△COP のとき、△AOB＝△AOP |
 |
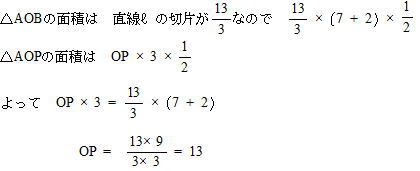| 答 （13，０） |
