筑波大学付属高等学校過去問研究
2014年度筑波大学付属高等学校数学入試問題は 例年通り大問4題構成。1.小問集合7問 2.平面図形(台形) 3.平面図形(円の性質) 4.空間図形 で、図形を中心とした出題構成も例年通りでした。
今回は 筑波大学付属高校入試頻出の 3.平面図形 を解説します。補助線をどう引くかを工夫して、相似比を用いて解いていきましょう。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


2014年度筑波大学付属高等学校数学入試問題は 例年通り大問4題構成。1.小問集合7問 2.平面図形(台形) 3.平面図形(円の性質) 4.空間図形 で、図形を中心とした出題構成も例年通りでした。
今回は 筑波大学付属高校入試頻出の 3.平面図形 を解説します。補助線をどう引くかを工夫して、相似比を用いて解いていきましょう。

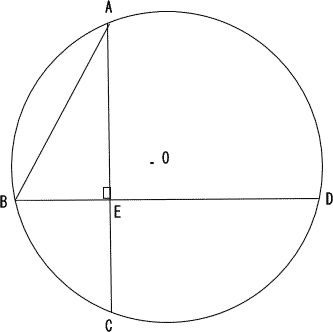
| (1) 線分ADの長さは⑩cmである。 |
| 解説 |
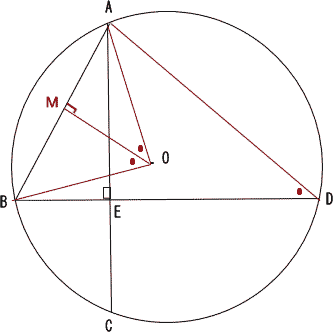 |
| 点A,O, 点B,Oを直線で結ぶ。 円の中心OからABに垂線をおろす。二等辺三角形の頂点の二等分線は底辺を垂直に二等分するので ∠AOM = ∠BOM ∠AOB = 2∠ADB (弧ABの中心角と円周角)なので ∠AOM = ∠BOM = ∠ADE よって △AOMと△ADEにおいて、∠AOM = ∠ADE,∠AMO = ∠AED = 90° 二角相等なので ∠AOM ∽ ∠ADE 三平方の定理より 相似比より 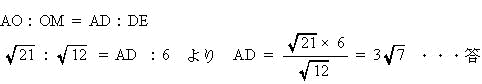 |
| (2) 弦ACの長さは⑪cmである。 |
| 解説 |
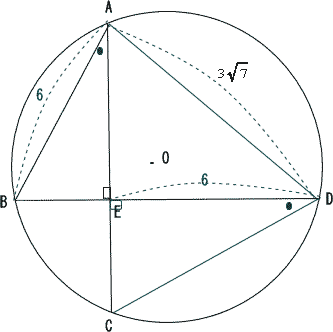 |
| 三平方の定理より △BAEと△CDEにおいて ∠BAE = ∠CDE (弧BCの円周角), ∠AEB = ∠DEC = 90° 二角相等より △BAE ∽ △CDE 辺の比より 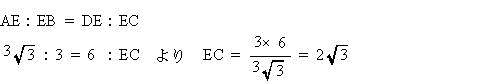 |
| (3) 2直線EO,ADの交点をFとするとき、線分EFの長さは、⑫cmである。 |
| 解説 |
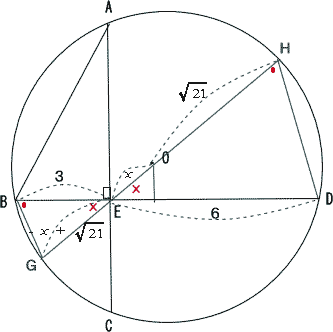 |
| EDを延長し、円Oの円周との交点をそれぞれG,Hとおく。 △BGEと△HDEにおいて、∠EBG = ∠EHD(弧GDの円周角),∠BEG = ∠HED(対頂角)二角相等なので △BGE∽△HDE GE:EB = EB = DE:EH より 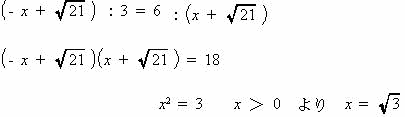 |
円の中心OからBDに垂線を下ろし、その交点をNとする。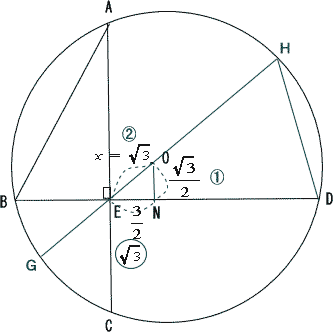 BN = ND なので 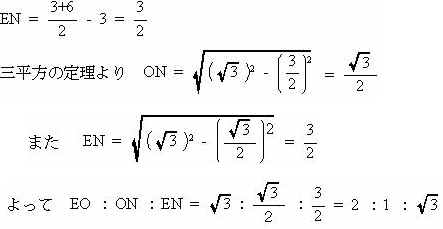 |
FからBDに垂線を下ろしその交点をPとおく。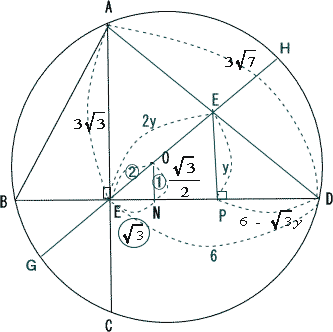 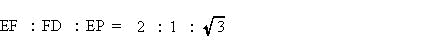 |