���Z�w�����v���ƒ닳�t�̒}�g��w�t����ꍂ���w�Z�ߋ��⌤��
�}�g��w�t����ꍂ���w�Z�w���̓X�y�[�X�n�m�d�̃v���ƒ닳�t�ɂ��C�����������B
 |
���˗���p�_�C���� |
0120-604-405 |
| ���₢���킹 |
03-6868-6040 |
 |
���₢���킹���[��
|
|
 |
ws-spaceone |
|
�v���ƒ닳�t�W�c�X�y�[�XONE
 HOME
HOME
2014�N�x�}�g��w�t����ꍂ���w�Z�������(�ߋ���) ���
�}�g��w�t����ꍂ���w�Z�ߋ��⌤��
�}�g��w������ꍂ���w�Z2014�N�x���w�������́A��N�ʂ菬��W���̂Ȃ����S��\���ł����B
�o����e����N�ʂ�@�P�D�ꎟ�����̃O���t�Ɛ}�`�i�}��R�j�@�@�Q�D���̐����i�}��R�j�@�R�D���ʐ}�`�i�}��R�j�@�S�D��Ԑ}�`�i�}��3�j�ł����B�e���Ƃ��@(1)(2)�͉����₷�����ł����A(3)�͓�⑵���ł��B���p���x���̖����J��Ԃ��w�K���{�Ԃɔ����܂��傤�B
����́@�R�D���ʐ}�`�i�}��R�j��������܂��B�⏕�����g���ċ��߂Ă����܂��傤�B
���w�������@�R�D���ʐ}�`
���@3
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
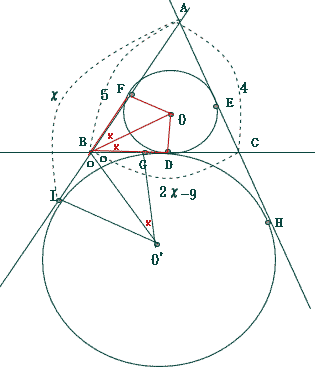
�_O�𒆐S�Ƃ��锼�arcm�̉~O�ƁA�_O'�𒆐S�Ƃ���ό`r'cm�̉~O'������AOO'��(r + r')cm�ł��B�������Ar��r'�Ƃ��܂��B
�}�̂悤�ɁA�Q�̉~O�CO'�ɐڂ��钼��BC�CCA�CAB������A�R�_D�CE�CF�͂����̒����Ɖ~O�̐ړ_�C�R�_G�CH�CI�͂����̒����Ɖ~O'�̐ړ_�ł��B�܂��AAB
= 5cm�CCA = 4cm�ł��B�@AF + BD + CE = ��cm�Ƃ��āA���̖₢�ɓ����Ȃ����B |
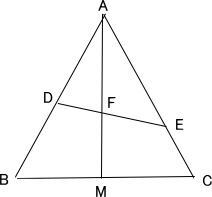 |
| (1)�@����BC,AI�̒��������ꂼ��Ԃ̎��ŕ\���Ȃ����B |
(2) (�A) ��OBO'�̑傫�������߂Ȃ����B
�@�@(�C)r��r'�̐�rr'���Ԃ̎��ŕ\���Ȃ����B |
| (3)�@rr' = 12 �̂Ƃ��A��ABC�̖ʐς����߂Ȃ����B |
|
 |
 |
 |
 |
t |
 |
 |
 |
 |
 |
�X�y�[�X�n�m�d�v���ƒ닳�t�̉ŁA�}�g��w�t����ꍂ���w�Z�̔��\�ł͂���܂���B
�@
(1) �����
| (1)�@����BC,AI�̒��������ꂼ��Ԃ̎��ŕ\���Ȃ����B |
|
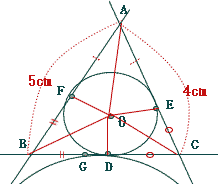
| ����BC�̒����@����� |
|
�@�~�O�̂P�_���炻�̉~�Ɉ������Q�̐ڐ��̒����͓������B�i�ڐ��̑Ώ̐��j
����AAF = AE�CBD = BF�CCE = CD�@
AF + BD + CE + AE + BF + CD = 2��
�܂��AAB = AF + BF = 5cm
AC = AE + CE = 4cm
AF + BD + CE + AE + BF + CD = 2��
5 + 4 + BD + CD = 2��
BD + CD = BC = 2��- 9
�@ |
 |
|
|
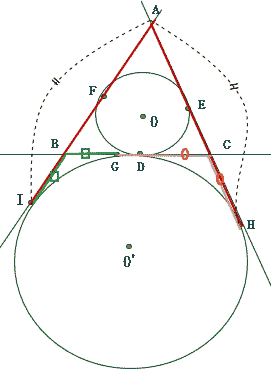
| ����AI�̒����@����� |
|
�~O'�ɂ����āA�ڐ��̑Ώ̐����@BI = BG�CCH = CG�CAI = AH
AI = AH = AB + BG + AC + CG = AB + AC + (BG + CG) = 5 + 4 + BC = 5 + 4
+ 2��- 9 = 2��
AI + AH = 2AI = 2��
���������ā@AI = �� |
 |
|
|
| ���@�@BC = 2��- 9�C�@�@�@AI = �� |
|
|
|
(2)�@����@
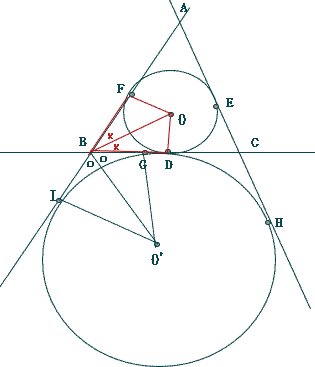
| (2) (�A) ��OBO'�̑傫�������߂Ȃ����B�@�@ |
|
| ����� |
|
��OFB�Ɓ�ODB�ɂ����āA
OF = OD (���a)�CFB = DB(�ڐ��̑Ώ̐�)�CBO = BO(����)
�Ή�����O�ӂ����ꂼ�ꓙ�����̂Ł�OFB �� ��ODB
�]���ā@��FBO = ��DBO�@�E�E�E�@
���l�Ɂ@��O'GB �� ��O'IB
�]���ā@��GBO' = ��IBO'�@�E�E�E�A
��FBO + ��DBO + ��GBO' + ��IBO' = 180��
(��FBO + ��IBO') + (��DBO + ��GBO') = 180��
�@�C�A���
(��FBO + ��IBO') = (��DBO + ��GBO') �Ȃ̂�
��OBO'�@= ��DBO + ��GBO' = 180��2 = 90��
|
 |
| ���@�@�@�X�O�� |
|
|
|
| �ʉ� |
|
�~O�́�ABC�̓��ډ~�Ȃ̂ŁA���S�͎O�p�`��3�̓��p�̓����̌�_�ł��邱�Ƃ���A�@��FBO = ��DBO�@�E�E�E�@
���l��BO�́�GBI�̓����Ȃ̂ŁA��GBO' = ��IBO'�@�E�E�E�A
�@�C�A���
(��FBO + ��IBO') = (��DBO + ��GBO') �Ȃ̂�
��OBO'�@= ��DBO + ��GBO' = 180��2 = 90��
���@�@�@�X�O��
|
 |
|
|
| (�C)r��r'�̐�rr'���Ԃ̎��ŕ\���Ȃ����B |
|
| ����� |
|
(�A)���@��OBO'�@= ��DBO + ��GBO' = 90��
����ā@��DBO = 90��- ��GBO' �E�E�E�@
�܂��@��GBO'�́@��O'GB = 90���Ȃ̂Ł@��BO'G = 90��- ��GBO'�@�E�E�E�A
�@�C�A���@�� DBO�Ɓ�GO'B�͒��p�Ƒ��̉s�p���������̂Ł@�� DBO �� ��GO'B
����ā@OD �FBG = DB �FGO' �E�E�E�B
FB + DB = (AB + BC + CD) - ( AF + AE + EC + DC)
AF = AE ,�@EC = DC �Ȃ̂Ł@AF + AE + EC + DC = 2(AE + EC) = 2C ���
FB + DB = AB + BC + CD - 2C = 5 + (2�� - 9) + 4 - 2�~4 = 2�� - 8
FB = DB �Ȃ̂Ł@DB = (2�� - 8)��2 = �� - 4
OD = r ,�@DG = r' ,�@BG = IB = �� - 5 , DB = �� - 4 ���B�ɑ������
r �F (�� - 5) = (�ԁ@- 4) �Fr'
�����̐� = �O���̐ρ@���
r r' = (�� - 5)(�ԁ@- 4) = ��2 - 9�� + 20 �E�E�E��
|
 |
|
|
(3)�@����@
| (3)�@rr' = 12 �̂Ƃ��A��ABC�̖ʐς����߂Ȃ����B |
|
| ����� |
|
(2)(�A)��� rr' = ��2 - 9�� + 20 = 12
��2 - 9�� + 8 = 0
(��- 8 )(��- 1) = 0 �@�@�� = 1,8
2�� - 9�� 0 �Ȃ̂Ł@�� = 8
���������ā@BC = 2�� - 9 = 2�~8 - 9 = 7
BF = BD = ��- 4 = 8 - 4 = 4
AI = �� = 8
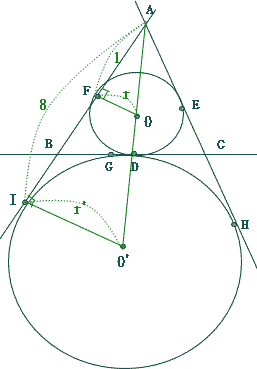
�܂��@��AOF�Ɓ�AO'I�ɂ�����
��OFA = ��O'IA = 90��
��FAO = ��IAO' (����)�@��p�����Ȃ̂Ł@��AOF �� ��AO'I
OF�FO'I = FA �FIA
OF = r ,O'I = r' �Ȃ̂�
r�Fr' = (5-4)�F8 = 1�F8
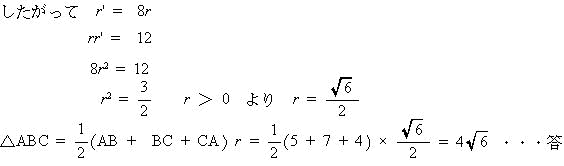 |
 |
|
|
HOME
Copyright(c)2007All Rights Rserved.
���̃z�[���y�[�W�̂��ׂĂ̕��͂̕��ӂ���ђ��쌠�̓v���ƒ닳�t�W�cSPACE ONE�ɑ����܂��B

