和歌山県立高等学校数学過去問研究
今回は和歌山県立高校の円と三平方の定理の問題を解説します。中心角・円周角・三平方の総合問題です。
和歌山県立高校 過去問対策
今回は和歌山県立高校の円と三平方の定理の問題を解説します。中心角・円周角・三平方の総合問題です。
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
今回は和歌山県立高校の円と三平方の定理の問題を解説します。中心角・円周角・三平方の総合問題です。
和歌山県立高校2010年度 数学入試問題 5. 平面図形(円の性質) 問題
 |
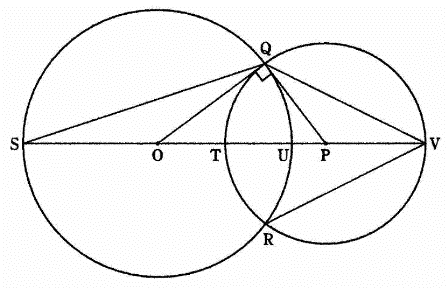| ４点 Ｓ，Ｔ，Ｕ，Ｖは，２つの円の中心Ｏ，Ｐを通る直線と円との交点である。 また，ＯＰ＝５㎝，∠ＯＱＰ＝90°である。 次の〔問１〕～〔問４〕に答えなさい。 |
| 〔問１〕 ＴＵの長さを求めなさい。 〔問２〕 ∠ＯＰＱ＝a°のとき，∠ＯＳＱの大きさをaの式で表しなさい。 〔問３〕 ∠ＯＰＱ＝∠ＱＶＲであることを証明しなさい。 〔問４〕 △ＯＱＳの面積を求めなさい。 |
和歌山県立高校2010年度 数学入試問題 5. 平面図形(円の性質) 問1 解説解答
| 問1 ＴＵの長さを求めなさい。 |
| 解説 |
 |
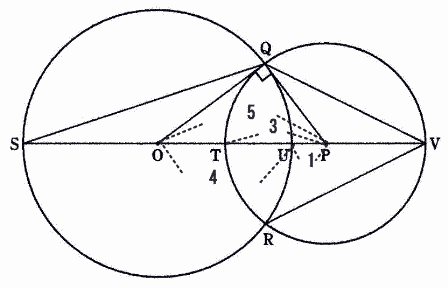| OP = 5cm OU(円Ｏの半径) = 4cm UP = OP - OU = 5 - 4 = 1cm TU = TP( 円Ｐの半径) = - UP = 3-1 = 2cm |
| 答 ２ｃｍ |
和歌山県立高校2010年度 数学入試問題 5. 平面図形(円の性質) 問2 解説解答
| 問2 ∠ＯＰＱ＝a°のとき，∠ＯＳＱの大きさをaの式で表しなさい。 |
| 解説 |
 |
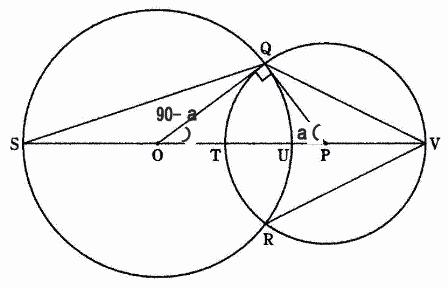| △OQPは∠OQP = 90°の直角三角形なので、 ∠QOT = 90 - a ・・・ 弧QUの中心角  |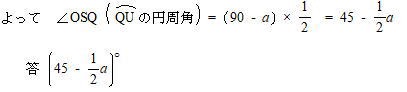
和歌山県立高校2010年度 数学入試問題 5. 平面図形(円の性質) 問3 解説解答
| 問3 ∠ＯＰＱ＝∠ＱＶＲであることを証明しなさい。 |
| 解答 |
 |
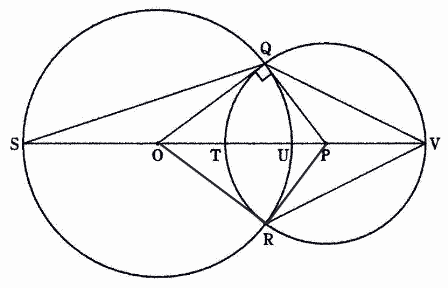| O とR，PとR を結ぶ。 △ OPQ と△ OPR において， OP＝ OP （共通） ・・・① OQ＝ OR （円O の半径） ・・・② PQ＝ PR （円P の半径） ・・・③ ①，②，③から，３辺が，それぞれ等しいので， △ OPQ ≡△ OPR よって，∠ OPQ ＝∠ OPR ・・・④ また，∠ QPR＝∠ OPQ+ ∠ OPR ・・・⑤ 円周角の定理から，∠ QVR ＝1/2∠ QPR ・・・⑥ ④，⑤，⑥から，∠ OPQ ＝∠ QVR |
和歌山県立高校2010年度 数学入試問題 5. 平面図形(円の性質) 問4 解説解答
| 問4 △ＯＱＳの面積を求めなさい。 |
| 解説 |
 |
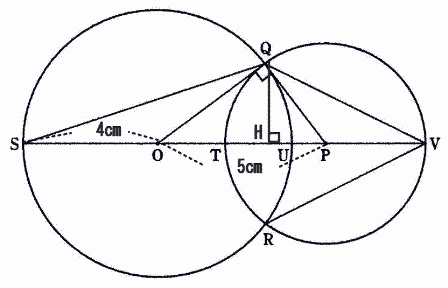| 点Ｑから辺ＯＰに垂線をおろし、直線ＯＰとの交点をＨとする。 |
| △ＯＰＱの面積は ＯＰ×ＰＱ÷２＝ＯＰ×ＱＨ÷２なので |
| ＱＨ＝４×３÷５＝２．４ |
| △ＳＯＱの面積は ＳＱ×ＱＨ÷２ より |
| ４×２．４÷２＝４．８ |
