杏林大学医学部過去問研究2009年度数学入試問題Ⅰ
こんにちは。医学部受験担当プロ家庭教師の福島です。
杏林大学医学部数学入試問題は大問４題構成もオールマークシートの解答形式も例年通り。
難易度も標準的で、これも例年通りでした。
一次試験合格ラインは７５％以上とされていますが、難問がないぶん数学が得意な受験生はパーフェクトをねらいたいところですね。
杏林大学医学部 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
杏林大学医学部 2009年度 数学入試問題Ⅰ
医学部受験プロ家庭教師スペースONEの杏林大学医学部数学入試問題解説解答
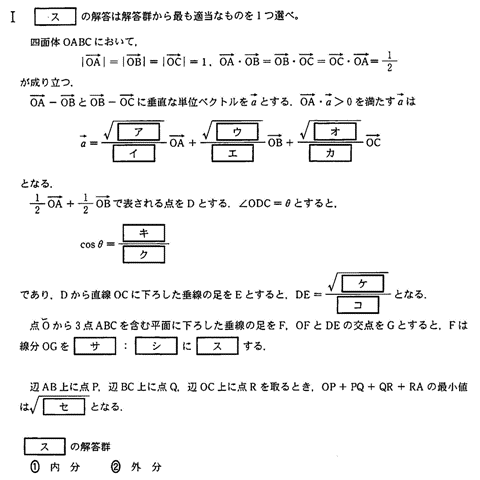
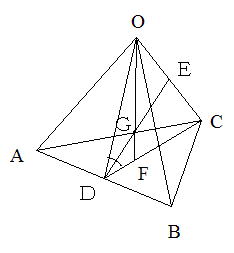
| ベクトルの与えられた条件から、この四面体がどのような四面体か考えます。 | ||
内積の条件から  |
||
 より、辺OAと辺OBのなす角は60°になる。 |
||
| 同様に 辺OBと辺OC、辺OCと辺OAのなす角も60°になる。各辺が等しいから △OAB, △OBC、△OCAはすべて正三角形になる。 よってこの四面体は右図のような正四面体である。 |
||
正四面体とわかったらその性質を活用することが、短時間に解答するこつですね。   に垂直な単位ベクトル を求めます。 |
||
 |
||
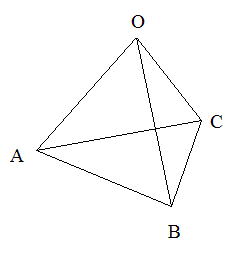
| 図のように頂点Oから△ABCにおろした垂線OFベクトルの単位ベクトルを求めればよい。 | ||
 |
||
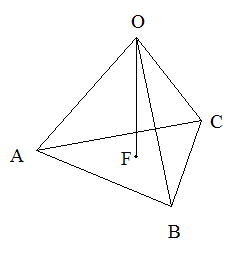
| 正四面体の性質から、点Ｆは△ABCの重心になります。これは覚えておきましょう。 |
||
 ……① |
||
単位ベクトルは |
||
 は正四面体の図からも求められますが、を平方して求めてみます。 |
||
 より  |
||
①に代入して となります。 |
||
| 問題のアからカまではすべて６になる。 | ||
 で表される点Ｄは辺ABの中点になる。 |
||
 |
||
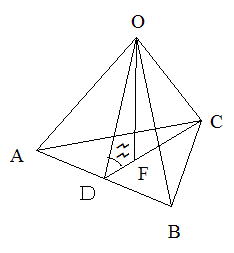
| 上の図のようになるので余弦定理を使っても求められますが、 内積を使って求めてみます。 |
||
 |
||
 ……② |
||
| また | ||
 |
||
 |
||
 |
||
| ゆえに | ||
 ……③ |
||
| ②、③より | ||
 |
||
 |
||
| 問題のキ、クはそれぞれ１，３になる。 | ||
| Ｄから直線ＯＣに下ろした垂線の足をＥとする。 | ||
| ここで△ＤＯＣはＤＯ＝ＤＣの二等辺三角形です。 | ||
| 三平方の定理で簡単にＤＥは求められます。 | ||
| ケ、コはともに２となる。 | ||
 |
||
| 図のようにＦは線分ＯＧの外側にあるので、Ｆは線分ＯＧを外分してます。 その比を求めるにはベクトルの1次独立を利用します。 |
||
 とおきます。 |
||
| ①より | ||
 ……④ |
||
| また、ＤＧ：ＧＥ＝ｔ：（１－ｔ）とおくと | ||
 |
||
 ……⑤ |
||
| ④、⑤より | ||
 |
||
 |
||
| これから | ||
  |
||
| ゆえにＯＧ：ＯＦ＝３：４よりＦは線分ＯＧを４：１に外分します。 サ、シ、スはそれぞれ４，１，②が入ります。 |
||
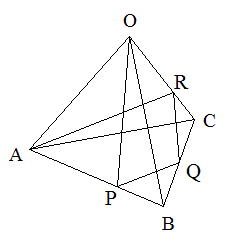
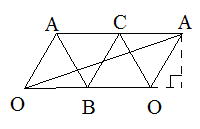
| 正四面体の各辺を通る最短距離は展開図を書いて求めれば簡単にできます。 | ||
 |
||
上図の展開図より、底辺は2.5、高さは の直角三角形の斜辺の長さがもとめる答えです。 |
||
 |
 |
|
| セは７です。 | ||
