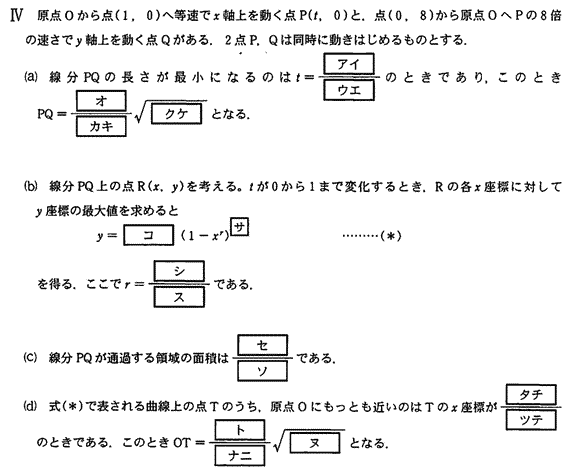
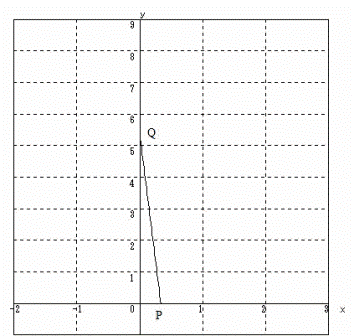
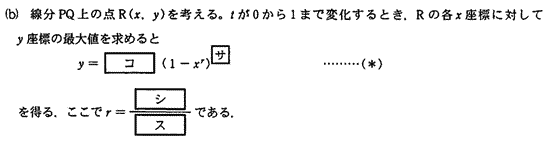
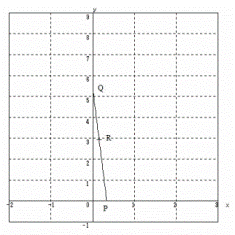
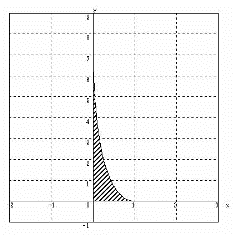
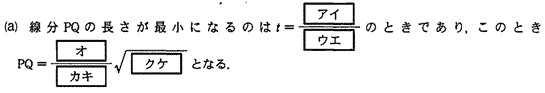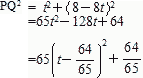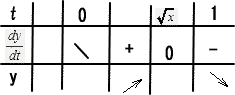杏林大学医学部過去問研究2010年度数学入試問題4
こんにちは。医学部受験数学指導プロ家庭教師の福島です。
杏林大学医学部数学入試問題は大問４題構成もオールマークシートの解答形式も例年通り。
難易度も標準的で、難問奇問もなくこれも例年通りでした。
出題内容はⅠ．余弦・正弦定理，ヘロンの定理による三角形の求積，内接円の半径と面積，領域上での変数関数の値域 Ⅱ．約数の個数と総和，三角関数の極限 Ⅲ．楕円の接線公式，接線の交点の軌跡 Ⅳ．積分による面積計算，微分による最小値でした。
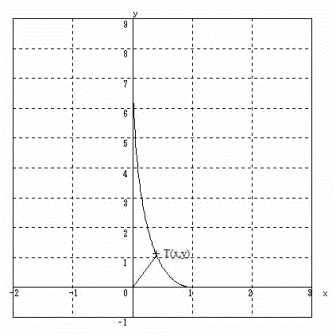
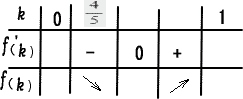
今回は Ⅳを解説します。
のとき最大値になる。
より、増減表を書くと
